[자료구조 1] 알고리즘 성능 분석부터 이해하기
[자료구조]시리즈 형식으로 다양한 자료구조를 정리하고자 포스팅합니다. 이 시리즈는 자료구조를 직접 구현해보는 것이 아닙니다. 알고리즘 문제해결 역량을 키우기 위해 자료구조의 특징들을 공부하면서 정리해놓은 글입니다.
알고리즘 성능 분석을 할 수 있어야 한다
어떤 자료구조가 어떤 상황에 쓰이는지를 이해하기 위해서는 반드시 알고리즘에 대한 성능 분석을 할 수 있어야 합니다. 다시말해 본인이 작성한 코드가 메모리를 얼마나 사용하고, 얼마나 빠른지 가늠할 줄 알아야 합니다.
여기서 다룰 내용은 작성한 코드가 필요한 메모리나 수행속도를 어떻게 측정할 것인가? 입니다.
‘몇초가 걸릴거야’ 라고 정확히 계산해내는 것은 당연히 어렵지만 가늠하는 것은 그렇게 어렵지 않습니다.
알고리즘의 성능은 어떻게 측정할까?
알고리즘 성능이 좋다/나쁘다에 대한 기준은 보통 아래 2가지로 결정됩니다.
- 어떤 알고리즘이 더 빠른가?
- 어떤 알고리즘이 메모리를 더 적게 사용하는가?
어떤 문제를 풀때 여러가지 알고리즘으로 같은 문제를 풀 수 있습니다. 하지만 다양한 알고리즘으로도 같은 결과를 낼 때 우리는 더 처리 속도가 빠르고 더 적은 메모리를 사용하는 알고리즘을 만들어야 합니다. 컴퓨터의 자원은 곧 돈이니까요.
이를 판단하기 위해 시간 복잡도(Time Complexity), 공간 복잡도(Space Complexity)라는 것을 사용합니다.
- 시간 복잡도(Time Complexity): 어떤 문제를 해결하기 위해 필요한 연산의 양을 수식으로 표현
- 공간 복잡도(Space Complexity): 어떤 문제를 해결하기 위해 필요한 메모리의 양을 수식으로 표현
알고리즘 문제풀이에서 크게 신경쓸 부분은 수행속도이기도 하고, 시간복잡도 개념을 이해하면 공간복잡도도 자연스럽게 알게 되기 때문에 시간복잡도에 대한 개념의 관점에서만 이해해보고자 합니다.
시간 복잡도(Time Complexity) 이해하기
문제) N개의 수가 주어질 때 숫자 0이 존재하는가?
ex1. (N=10) : 0, 5, 10, 492, 20, 5, 9, 3, 1, 5
ex2. (N=8) : 3, 5, 1, 9, 4, 11, 25, 0
위 문제를 보고 가장 직관적인 알고리즘은 주어진 수를 한번씩 확인하는 것입니다.
1번 같은 경우는 바로 찾을 수 있고, 2번 같은 경우는 모두 확인해야 알 수 있습니다. 즉 입력이 무엇이 들어오느냐에 따라 수행속도가 크게 달라집니다.
1번과 같은 경우를 Best Case(최선의 경우)라고 하고, 2번을 Worst Case(최악의 경우)라고 합니다. 보통 최악의 경우를 기준으로 알고리즘 성능을 판단합니다.
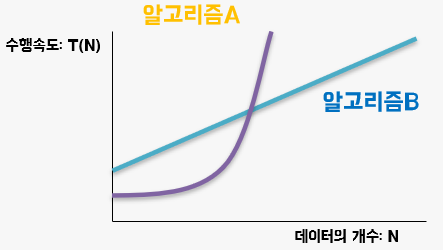
그리고 입력 값의 변화 말고도 N의 크기에 따라서도 수행속도가 크게 달라집니다.
위의 그림에서 알고리즘 A와 B 중 무엇이 좋은 알고리즘 일까요?
수행속도의 관점에서는 N이 작을 때는 알고리즘 A가 좋고, N이 크면 알고리즘 B가 좋지만, 일반적으로는 B가 더 좋아보입니다.
위에서 말한 두 가지를 정리하면 다음과 같습니다.
- 주어진 입력에 따라 연산량이 다름
=> 최악의 경우(Worst Case)를 기준으로! - 문제 제약조건(N의 최대크기 등)에 따라 좋은 알고리즘이 결정됨
=> N의 크기에 따른 수행속도로!
그래서 최악의 경우를 기준으로 변화하는 N의 값을 통해 시간복잡도를 계산할 것입니다.
빅-오 표기법 (BigO Notation)
위의 문제에서 순차적으로 확인해보는 알고리즘은 최악의 경우 N번 확인해야 하기 때문에 “시간복잡도가 O(N)인 알고리즘이다” 라고 표현합니다.
이렇게 표현하는 것을 빅오 표기법이라고 하고, 독특하게도 수식의 상수배와 낮은 차항은 다 무시하고 최고차항만 취급합니다. 즉, 가장 영향력이 큰 수식만 고려하려는 것입니다.
예를 들어 코드의 시간복잡도가 아래 수식과 같을 때 상수배와 낮은 차항들은 다 버리고 표현합니다.
Case 1. T(N) = 3N^2 + 2𝑁 + 3 => O(N^2)
Case 2. T(N) = 8𝑁^3 + 14982𝑁 + 293 => O(𝑁^3)
Case 3. T(N) = 2^𝑁 + 8𝑁^4 => O(2^𝑁)
왜냐하면 N이 커질수록 수식에서 최고차항을 가장 영향이 크고, 낮은 차항에 상수배를 많이 해도 그 효과가 아주아주 작기 때문입니다. 다시 말해 수행속도는 최고차항에 해당하는 코드만 신경쓰면 됩니다.
조금 더 직관적으로 이해하기 위해 코드로 설명하면,
x = 1;
// 1. 상수항
for(int i=0; i<1000; i++)
x += i;
// 2. N차항
for(int i=0; i<N; i++)
x += 1
// 3. N^2차항
for(int i=0; i<N; i++)
{
for(int j=0; j<N; j++)
x += 1
}
위와 같은 코드가 있다고 하면, 여기서 N에 대해 수행속도에 대해 영향력이 큰 부분은 이중 for문입니다. 즉 N에 대한 2차식입니다. 그래서 1차식 for문과 위의 상수로 고정된 for문은 N의 크기에 관계없이 1000번의 연산이기 때문에 모두 무시합니다. 그 외에 기타 x=1 이라던지 N에 영향이 없는 연산들은 수행속도 계산에서 무시합니다.
믿기 어려울수도 있지만 정말로 시간복잡도를 얘기할 때는 빅-오(Big-O)를 사용합니다.
물론 상수항에 해당하는 연산이 많은 것도 수행속도에 큰 영향이 될 수도 있습니다. 하지만 빅오에서는 N이 충분히 클 때를 가정한 것이기 때문에 이렇게 접근하는 것입니다. 실제 현업에서는 빅-오 표기까지 바꿀만큼 알고리즘을 개선하기가 어렵기 때문에, 상수항 연산 개선도 중요합니다.
알고리즘 문제에서의 수행속도 계산
알고리즘 문제에서 내 알고리즘의 시간 복잡도를 알면 직접 돌려보지 않고도 “최악의 경우에도 실행가능하겠다”라는 판단 기준이 있습니다.
일반적으로 1억번의 연산당 1초 정도라고 계산하면 됩니다. 이를 토대로 문제가 어떤 시간복잡도를 가지는 알고리즘을 요구하는지 간단하게 알 수 있습니다.
문제 제약조건 별 요구하는 알고리즘
Case 1. [시간 제한 1초, N <= 1,000] : O(N^2) 또는 O(N^2*logN) 이하의 알고리즘 필요
Case 2. [시간 제한 1초, N <= 100,000] : O(N) 또는 O(NlogN) 이하의 알고리즘 필요
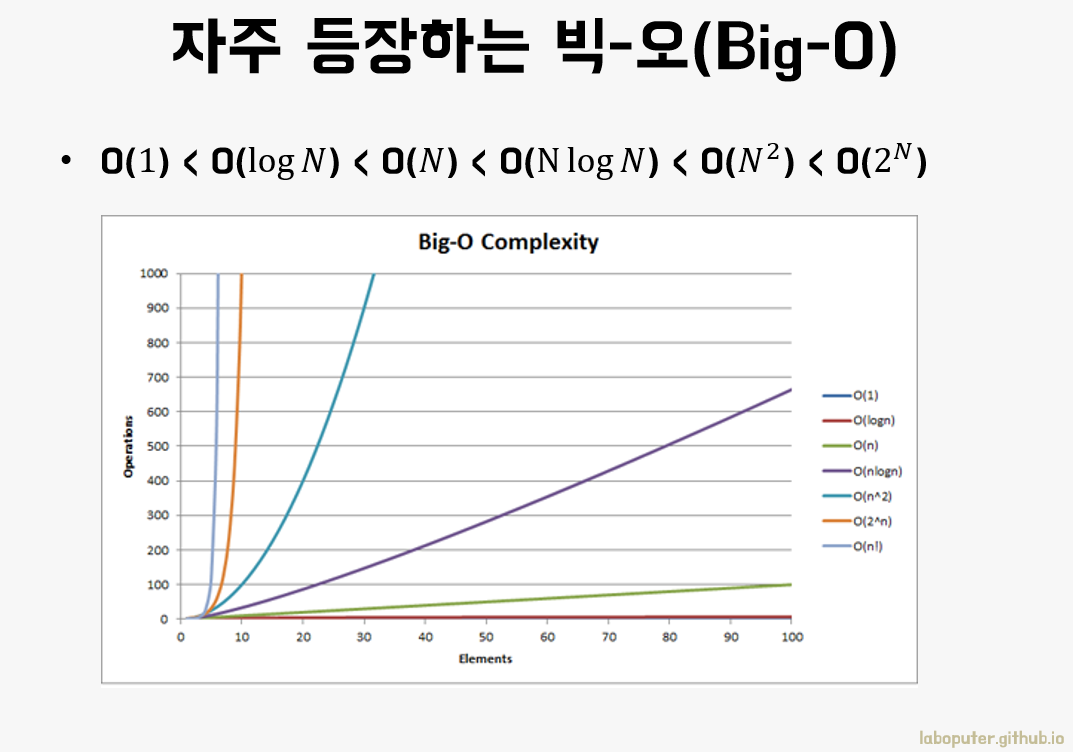
자주 사용하는 빅-오 표기법들
다행인 것은 알고리즘을 공부하고 문제은행식으로 훈련하는 과정에서는 위의 빅-오 표기법이 대부분입니다.
그래서 본인이 작성한 알고리즘의 성능이 무엇인지 몇번만 연습하면 쉽게 구하실 수 있을 것입니다.
성능이 좋다라는 기준을 알았으니 다음 장부터는 여러가지 자료구조를 구경해보죠!