[자료구조 1] 트리(Tree) 이해하기

트리(Tree)가 무엇이고 어디에 활용되는지 알아봅니다. 그리고 트리와 관련된 문제를 풀어봅니다.

트리 (Tree)

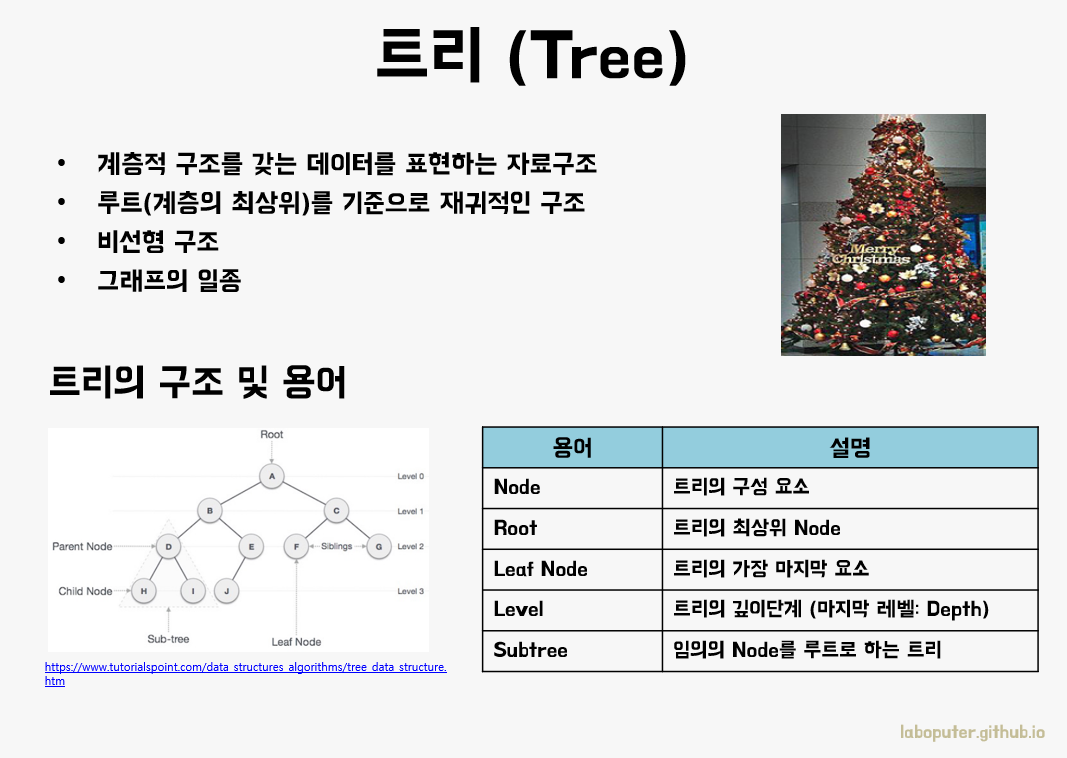
트리(Tree)는 대표적으로 계층적 구조를 표현하기 좋은 자료구조 입니다. 일반적인 데이터 저장은 선형적이었다면 트리는 비선형 구조로 계층적인 관계 표현을 하기가 수월해집니다. 그래서 트리를 어떻게 표현하는지 아래 그림에 나와있는 용어들에 익숙해지는 것이 좋습니다.

특히 트리는 이진 검색 트리, 우선 순위 큐, 세그먼트 트리 등으로 다양하게 응용하여 알고리즘 문제를 해결하는데 큰 도움이 됩니다.

트리의 종류

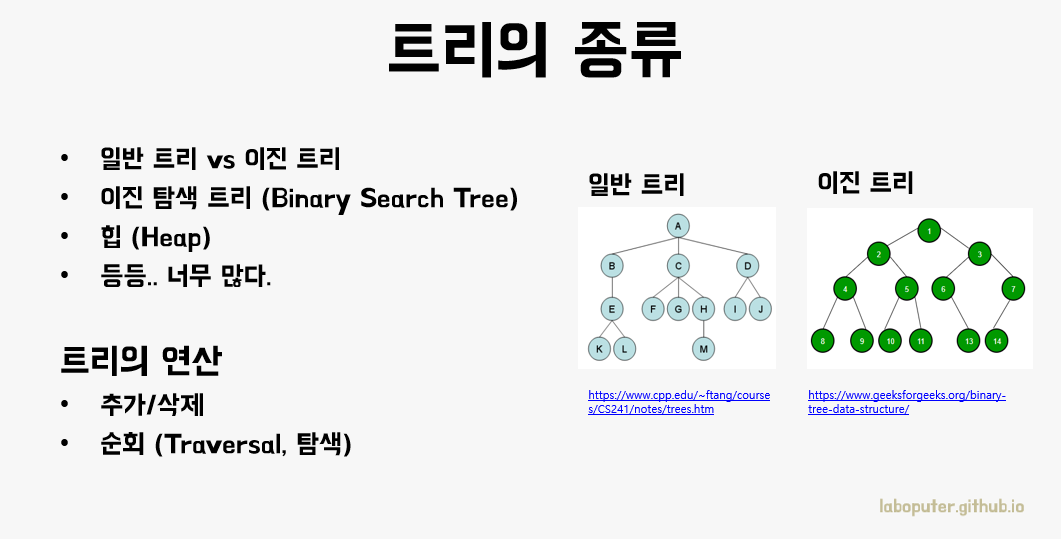
트리는 종류가 굉장히 다양합니다. 트리의 구조를 조금 변형하여 특정 연산에 효율적인 동작을 할 수 있도록 한 경우가 많기 때문입니다.

트리의 하위 노드가 최대 2개인 경우에는 이진 트리(Binary Tree)라 불립니다. 그 외에도 리프 노드를 제외한 모든 노드의 하위 노드가 2개인 경우 포화이진트리(Full Binary Tree)라고도 합니다. 트리의 구조에서 이진 트리는 하위 노드가 2개 밖에 없기 때문에 구현도 상대적으로 쉽고 연산도 빠르기 때문에 자주 사용합니다.

트리에서 가장 중요하고 기본적인 연산은 탐색(순회)입니다. 모든 노드를 한번씩 확인하는 작업은 자주 쓰이는 것이기 때문입니다.

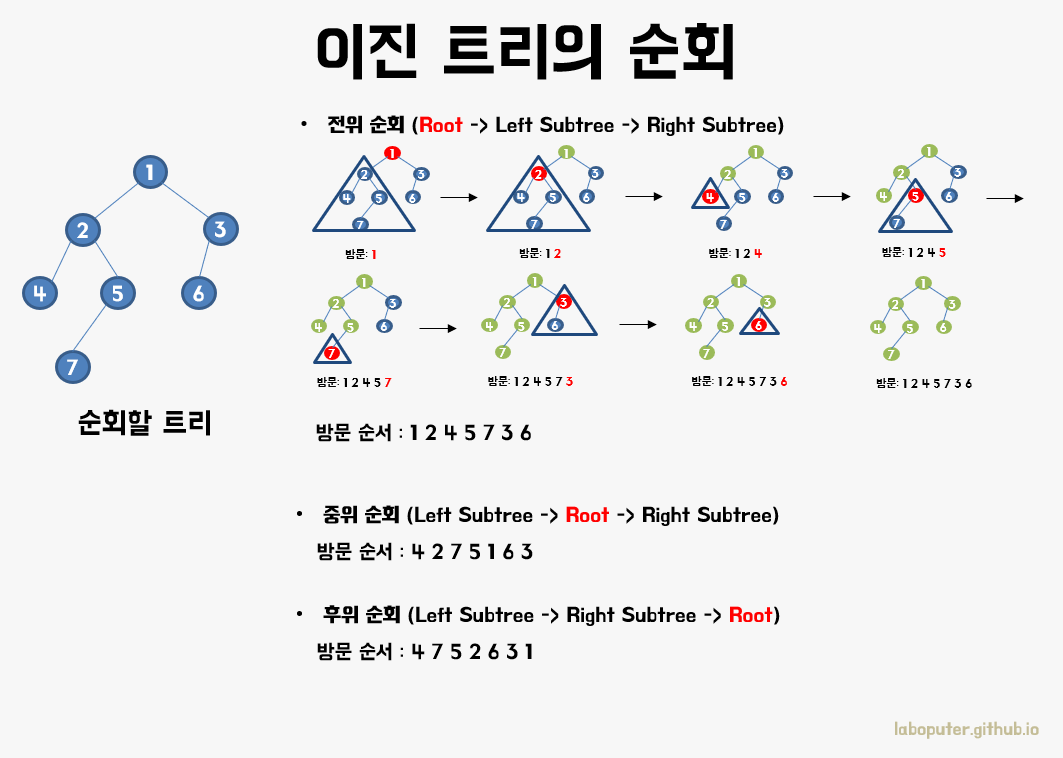
그 중에서도 이진 트리의 연산하면 늘 나오는 순회 3가지가 있습니다.

전위 순회(Preorder Traversal): (루트) -> 왼쪽 서브트리 -> 오른쪽 서브트리
중위 순회(Inorder Traversal): 왼쪽 서브트리 -> (루트) -> 오른쪽 서브트리
후위 순회(Postorder Traversal): 왼쪽 서브트리 -> 오른쪽 서브트리 -> (루트)

각각의 순회는 루트 노드를 언제 방문하느냐가 다르며, 연산의 시간복잡도는 모두 O(N)으로 동일합니다.

포스팅 마지막에 예제로 직접 풀어볼 것입니다.

트리의 활용

트리처럼 계층적인 구조가 필요한 경우는 생각보다 많습니다.

위 그림처럼 우리가 컴퓨터에서 늘 쓰고 있는 폴더와 파일들도 트리로 표현할 수 있습니다. 특히 DB에서 원하는 데이터를 빠르게 찾아내거나 하는 작업들도 트리 구조를 이용하기도 합니다. 그리고 트리는 트리의 하위 노드는 서브 트리로써 구성되어 있기 때문에, 프로그래밍에서도 재귀를 통해 쉽게 연산을 구현할 수 있어서 직관적입니다.

예제: 트리 순회

문제 링크:: 트리순회 문제(https://www.acmicpc.net/problem/1991)

자세한 문제 설명은 위 링크로 들어가셔서 확인하시고 직접 풀어보세요!

가장 기본적인 연산인 탐색을 구현하는 문제로, 재귀로 풀면 코드 자체도 짧고 쉽게 푸실 수 있는 좋은 문제입니다.

풀이

전위 순회를 예로 들어 설명하면, 여기서 핵심적인 내용은 “(루트) -> 왼쪽 서브트리 -> 오른쪽 서브트리”로 각각의 트리를 다시 똑같이 방문해야한다는 점입니다. 즉 재귀로 풀면 쉽습니다.

중위 순회나 후위 순회는 Root의 방문 위치만 변경해주면 끝입니다.

아래와 같이 구현한 함수에서 Root로 시작하면 모든 노드를 탐색하게 됩니다.

#include <stdio.h>
using namespace std;

struct tree
{
	int left='.';
	int right='.';
};

tree tr[100];

void PreOrder(int i)
{
	if (i == '.')
		return;

   // Root 방문 후 Left Subtree, Right Subtree 각각 방문
	printf("%c", i);
	PreOrder(tr[i].left);
	PreOrder(tr[i].right);
}

void InOrder(int i)
{
	if (i == '.')
		return;

	InOrder(tr[i].left);
	printf("%c", i);
	InOrder(tr[i].right);
}

void PostOrder(int i)
{
	if (i == '.')
		return;

	PostOrder(tr[i].left);
	PostOrder(tr[i].right);
	printf("%c", i);
}

int main(void)
{
	int n; cin >> n;
	
	char root;
	char c1, c2, c3;
	scanf(" %c %c %c", &c1, &c2, &c3);
	root = c1;
	tr[c1].left = c2;
	tr[c1].right = c3;
	for (int i = 1; i < n; i++)
	{
		scanf(" %c %c %c", &c1, &c2, &c3);
		
		tr[c1].left = c2;
		tr[c1].right = c3;
	}

	PreOrder(root);
	printf("\n");
	InOrder(root);
	printf("\n");
	PostOrder(root);
	printf("\n");

	return 0;
}

다른 문제 추천

트리의 지름: (https://www.acmicpc.net/problem/1967)
트리의 높이와 너비: (https://www.acmicpc.net/problem/2250)

알고리즘 문제에서 트리를 사용해야 하는 경우가 많이 등장합니다. 물론 트리를 응용한 구조나 연산을 필요로 하기 때문에 기본적인 트리에 대한 이해를 하면 좋을 것 같습니다.