[자료구조 1] 그래프(Graph) 이해하기
그래프(Graph)가 무엇이고 어디에 활용되는지 알아봅니다. 그리고 그래프와 관련된 기초 문제를 풀어봅니다.
그래프 (Graph)
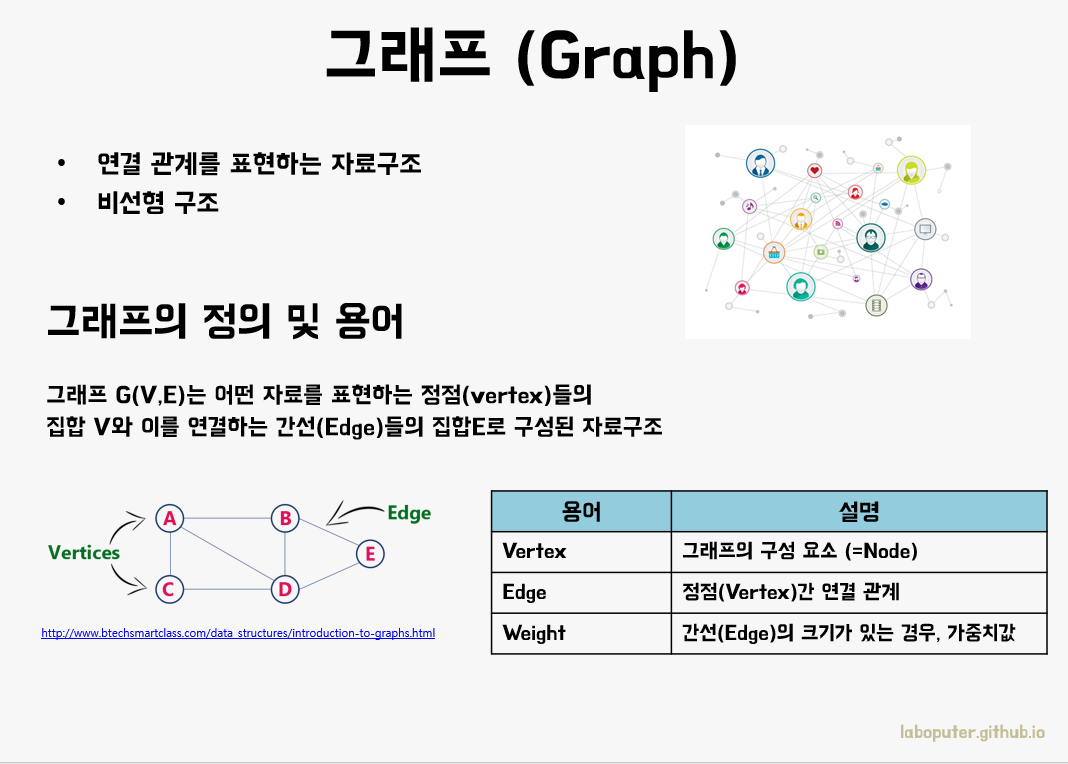
그래프(Graph)는 데이터 간의 관계를 표현하기 위한 자료구조입니다. 그래프 역시 비선형 구조이며, 트리의 일반적인 개념입니다. 트리도 일종의 그래프 중 하나에 속합니다.
그래프는 정점(Vertex)와 간선(Edge)로 이루어지며, 추상적인 개념이지만 현실세계에도 많이 나타나기 때문에 알고리즘 문제에서도 자주 등장합니다.
그래프의 종류
그래프도 역시 종류가 다양합니다.
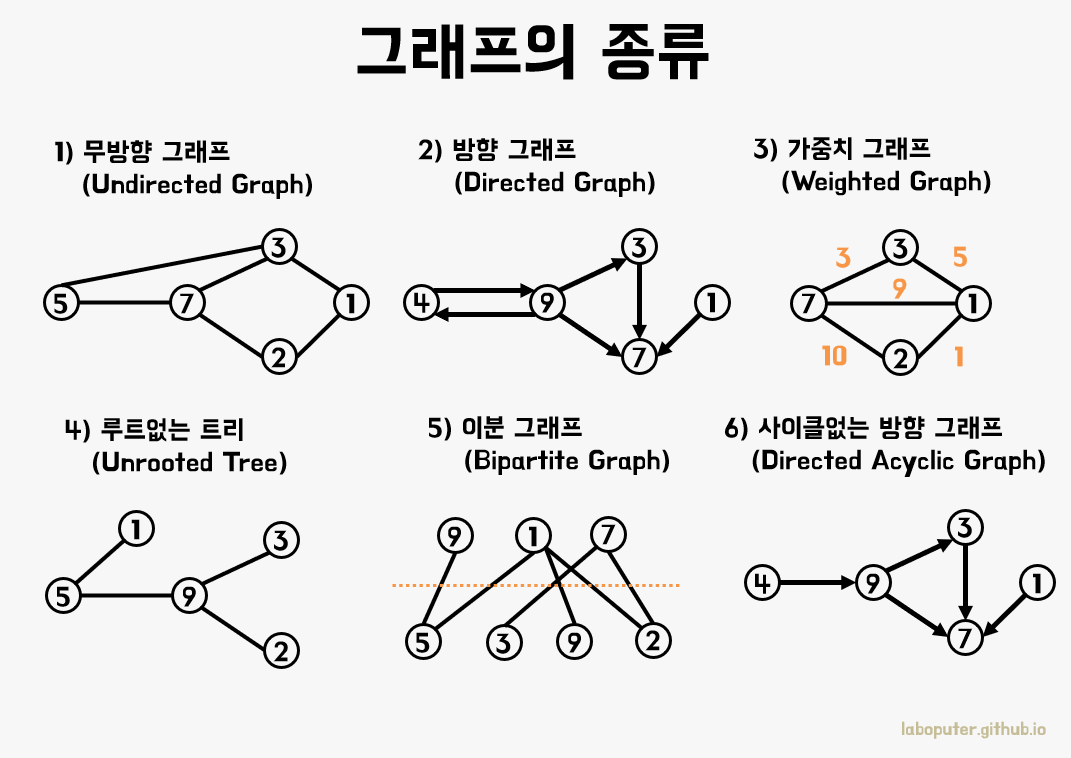
- 무방향 그래프: (간선의) 방향이 없는 그래프
- 방향 그래프: 방향성이 있는 그래프
- 가중치 그래프: 간선의 가중치값이 존재하는 그래프
- 루트없는 트리: 간선을 통해 정점 간 잇는 방법이 한가지인 그래프(
*트리의 정의) - 이분 그래프: 그래프의 정점을 겹치지 않게 두 그룹으로 나눈 후 다른 그룹끼리만 간선이 존재하게 분할할 수 있는 그래프
- 사이클이 없는 방향 그래프: 정점에서 출발해 자기 자신으로 돌아오는 경로(사이클)가 없는 그래프
각각의 그래프가 알고리즘 문제로도 자주 나올 정도이기 때문에 정리하였습니다. 이런 것이 있구나 이해만 해도 충분하지만 문제에서 나오면 각 그래프의 특징들을 찾아보시길 바랍니다.
그래프의 표현
그래프도 트리처럼 가장 대표적인 연산이 모든 정점을 탐색하는 것입니다. 단 그래프는 추상적인 개념이므로 코드상으로 어떻게 표현하는지부터 이해하는 것이 좋습니다.
크게2가지 방법으로 분류할 수 있습니다.
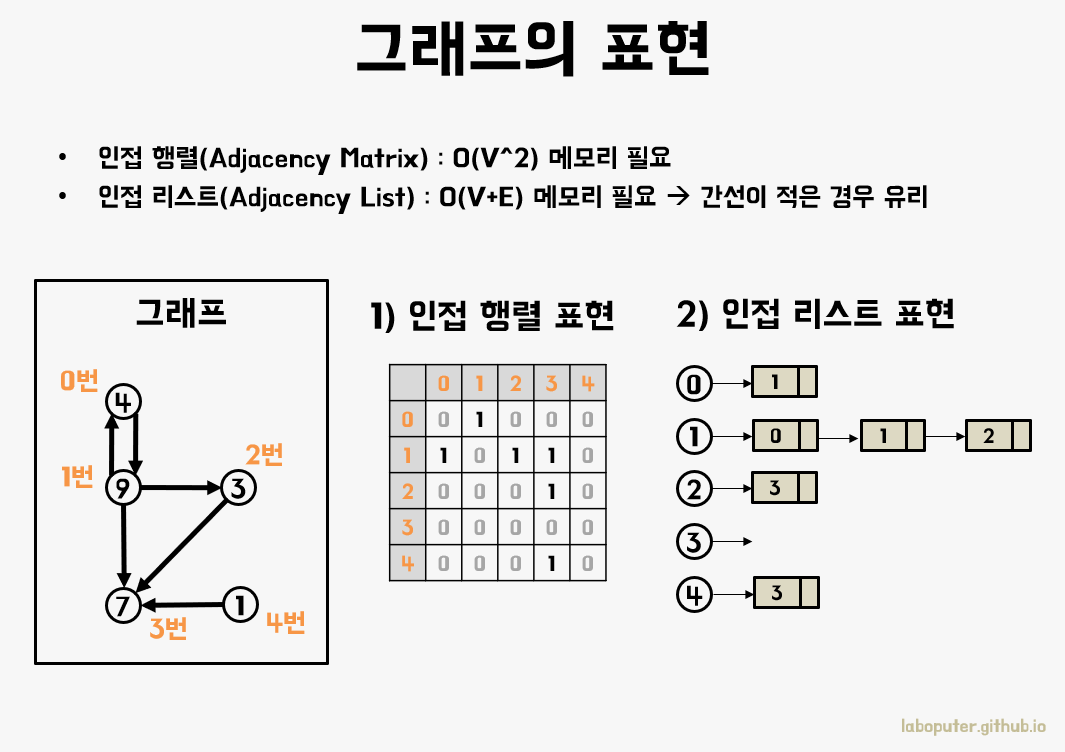
인접 행렬: 2차원 배열로 정점 간의 간선의 존재 여부를 1 또는 0
인접 리스트: 정점 개수만큼 리스트를 만들어 각각의 정점 리스트에 간선 추가
인접 행렬 표현은 항상 노드 개수의 제곱만큼 메모리(V^2)가 필요한데 이에 비해 간선이 매우 적으면 뭔가 비효율적임을 느끼실 것입니다. 탐색을 할 때도 연결되지 않은 간선들도 확인해야 되기 때문에 느립니다. 하지만 인접 리스트는 메모리도 조금만 사용(V+E)하며 탐색할 때도 연결된 간선만 보면 되기 때문에 빠릅니다.
그래프도 상황에 따라 배열과 리스트 중 무엇으로 구현할 지 선택해야 합니다.
그래프의 활용
그래프는 추상적이지만 생각보다 활용도가 높습니다. 관계 표현이 필요한 경우가 많기 때문입니다.
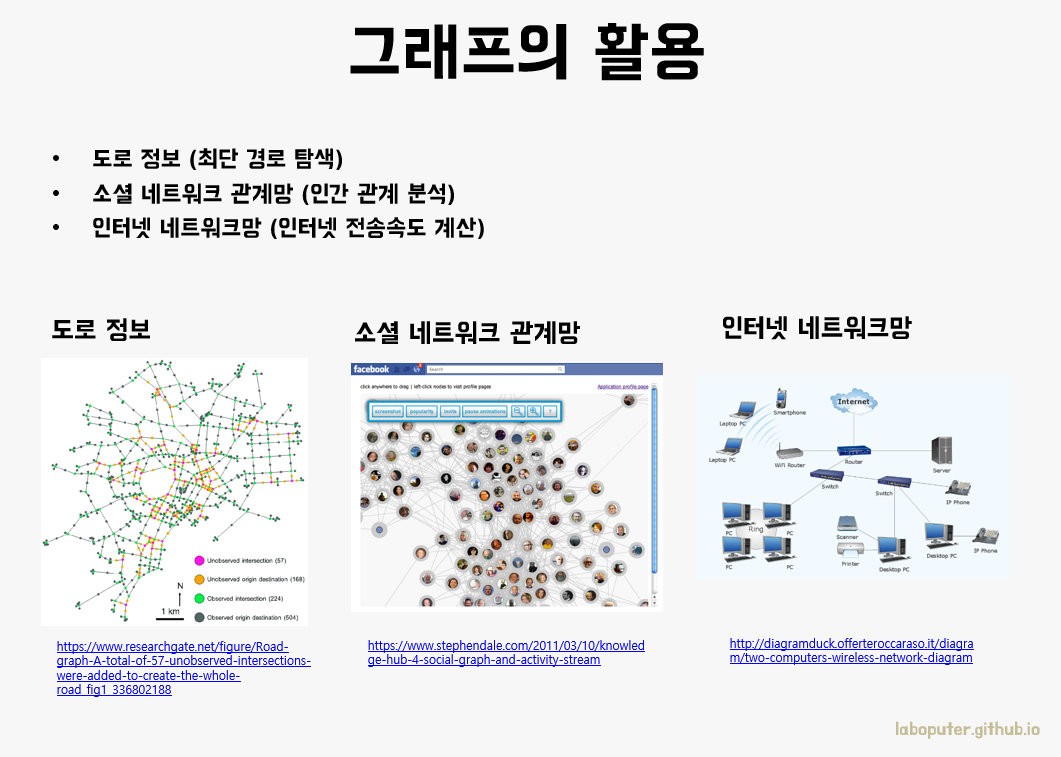
가장 대표적인 것이 최단 경로를 안내해주는 네비게이션입니다. 각 도시를 정점으로, 도로는 간선으로 표현하면 됩니다. 그리고 알고리즘 문제로 쉽게 등장하는 그래프에서의 최단 경로를 구하는 것도 어렵지 않습니다.
SNS에서의 인간 관계도 그래프로 표현하여 관계마다 친밀도를 구하거나 친구 추천 등의 서비스로도 이어질 수 있습니다.
인터넷 네트워크도 그래프로 표현하면 네트워크 회선마다 전송이 가능한 용량이 다를 때 컴퓨터에서 보내는 데이터를 어떤 케이블을 따라 보내야 할지 판단할 수도 있습니다.
예제: 바이러스
문제 링크:: 바이러스 문제(https://www.acmicpc.net/problem/2606)
자세한 문제 설명은 위 링크로 들어가셔서 확인하시고 직접 풀어보세요!
그래프에서 기초적인 문제로 그래프의 표현 방법을 알아야 하고 그래프에서 각 정점들을 어떻게 확인할 수 있는지 배울 수 있는 문제입니다.
풀이
이 문제는 정점의 수가 100으로 매우 작기 때문에 인접행렬과 인접리스트 중 편한 것으로 선택해도 큰 문제가 없습니다.
주어진 입력값으로 그래프를 표현했다면 실제로 1번과 연결된 모든 정점을 계속 방문하면서 개수만 카운트해주면 됩니다.
정점과 연결된 모든 정점을 방문하는 것을 각 정점마다 똑같은 행동을 해야하기 때문에 재귀로 구현하면 쉽겠다라는 생각을 할 수 있습니다. 사실 이 알고리즘은 DFS 입니다.
#include <stdio.h>
#include <vector>
#include <algorithm>
using namespace std;
#define MAXN 105
int N, M;
// 그래프의 인접리스트 표현
vector<int> vec[MAXN];
// 각 정점 방문 여부
bool visit[MAXN];
int rst = 0;
// v에서 시작해 연결된 정점을 방문하고, 연결된 정점으로 다시 시작
void DFS(int v)
{
for (int i = 0; i < vec[v].size(); i++)
{
if (!visit[vec[v][i]])
{
visit[vec[v][i]] = true;
DFS(vec[v][i]);
rst++;
}
}
}
int main(void)
{
scanf("%d%d", &N, &M);
for (int i = 0; i < M; i++)
{
int n1, n2; scanf("%d%d", &n1, &n2);
vec[n1].push_back(n2);
vec[n2].push_back(n1);
}
visit[1] = true;
DFS(1);
printf("%d\n", rst);
return 0;
}
다른 문제 추천
- 숨바꼭질: (https://www.acmicpc.net/problem/1697)
- 단지 번호 붙이기: (https://www.acmicpc.net/problem/2667)
- 섬의 개수: (https://www.acmicpc.net/problem/4963)
이번 포스팅까지가 자료구조 중 가장 기본적인 내용에 대해 정리하였습니다. 다음 포스팅부터는 이러한 기본적인 자료구조를 응용하여 특정 상황에 효과적으로 동작하는 자료구조들을 다뤄보겠습니다.