[자료구조 2] 우선순위 큐(Priority Queue) 이해하기
최댓값 또는 최솟값처럼 우선순위가 높은 데이터를 검색하는 연산만을 빠르게 하기 위해 고안된 자료구조로 우선순위 큐(Priority Queue)를 사용할 수 있습니다. 이 포스팅에서는 우선순위 큐가 무엇이고 어떻게 구현하는지를 예제를 통해 알아봅니다.
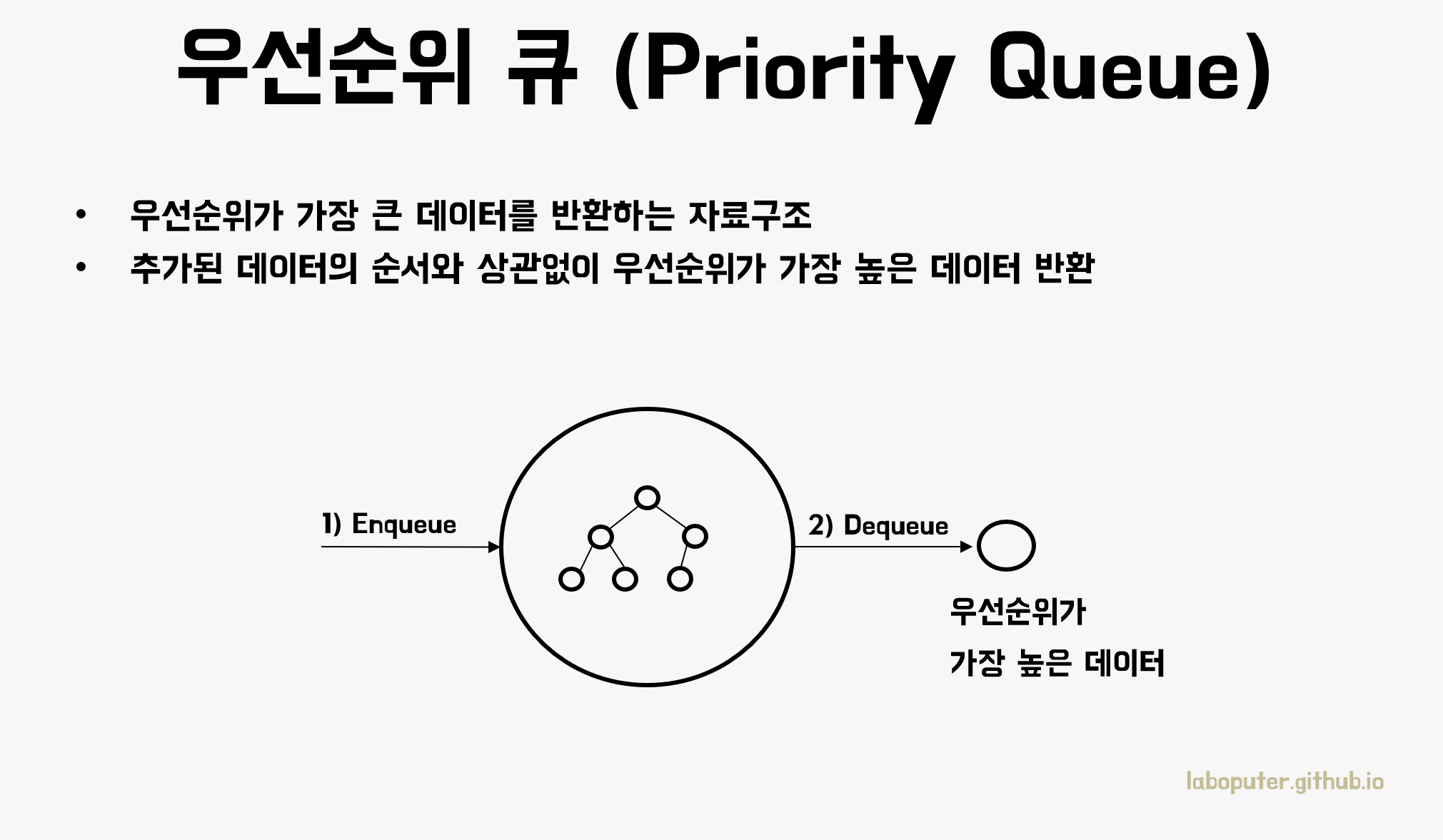
우선순위 큐(Priority Queue)
우선순위 큐는 이름처럼 우선순위가 가장 높은 데이터를 찾는 연산이 효율적인 자료구조입니다. 일반적인 큐처럼 추가/삭제 연산이 있지만 추가한 순서에 관계없이 삭제(또는 반환)를 하면 가장 우선순위가 높은 데이터를 가져올 수 있습니다. 그것도 아주 빠르게요.
시간복잡도
배열로 저장한 데이터에서 우선순위가 가장 높은 데이터를 찾는 것은 시간복잡도는 O(N)입니다. 물론 우선순위를 높은 데이터를 빠르게 찾아내는 방법도 있습니다. 데이터가 정렬되어 있다면 이진 탐색(Binary Search)을 통해 O(logN)도 가능합니다. 하지만 배열의 단점인 데이터를 추가하는 것은 O(N)입니다.
이제 알아볼 방법은 추가 연산도, 삭제 연산(우선순위 높은 데이터 탐색)도 모두 O(logN) 입니다.
힙 (Heap)
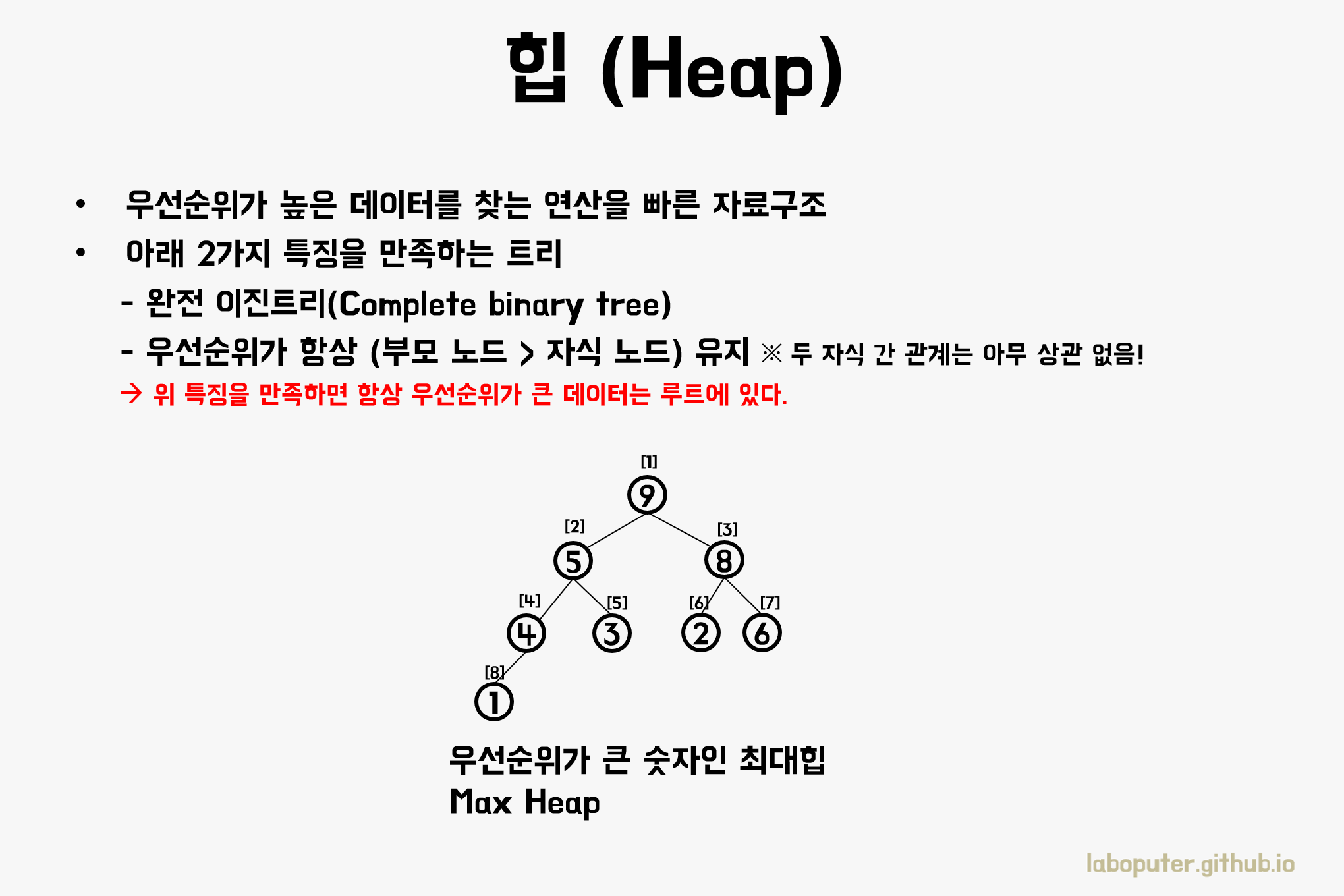
우선순위 큐는 힙이라는 트리로된 자료구조로 구현할 수 있습니다. 힙을 그대로 사용하면 우선순위 큐가 될 수 있기 때문에 앞으로는 힙을 기준으로 설명하겠습니다.
위 그림처럼 힙은 부모-자식 노드 간 우선순위가 유지된 완전이진트리입니다. 이 2가지를 만족하면 루트에는 항상 우선순위가 가장 높은 데이터가 있습니다.
그리고 완전이진트리(힙 포함)는 특성상 각 인덱스의 의미를 그림처럼 배열도 쉽게 표현도 가능하기 때문에 구현도 쉽습니다.
배열을 이렇게 취급하면 됩니다.
- 루트는 [1]에 있다.
- N개의 데이터는 [1]~[N]에 차례로 존재한다.
- 현재 노드 i를 기준, 왼쪽 자식 노드: [2i], 오른쪽 자식 노드: [2*i+1] 에 있다.
힙의 구현
힙의 2가지(추가, 삭제)연산에 대한 알고리즘을 알아보겠습니다.
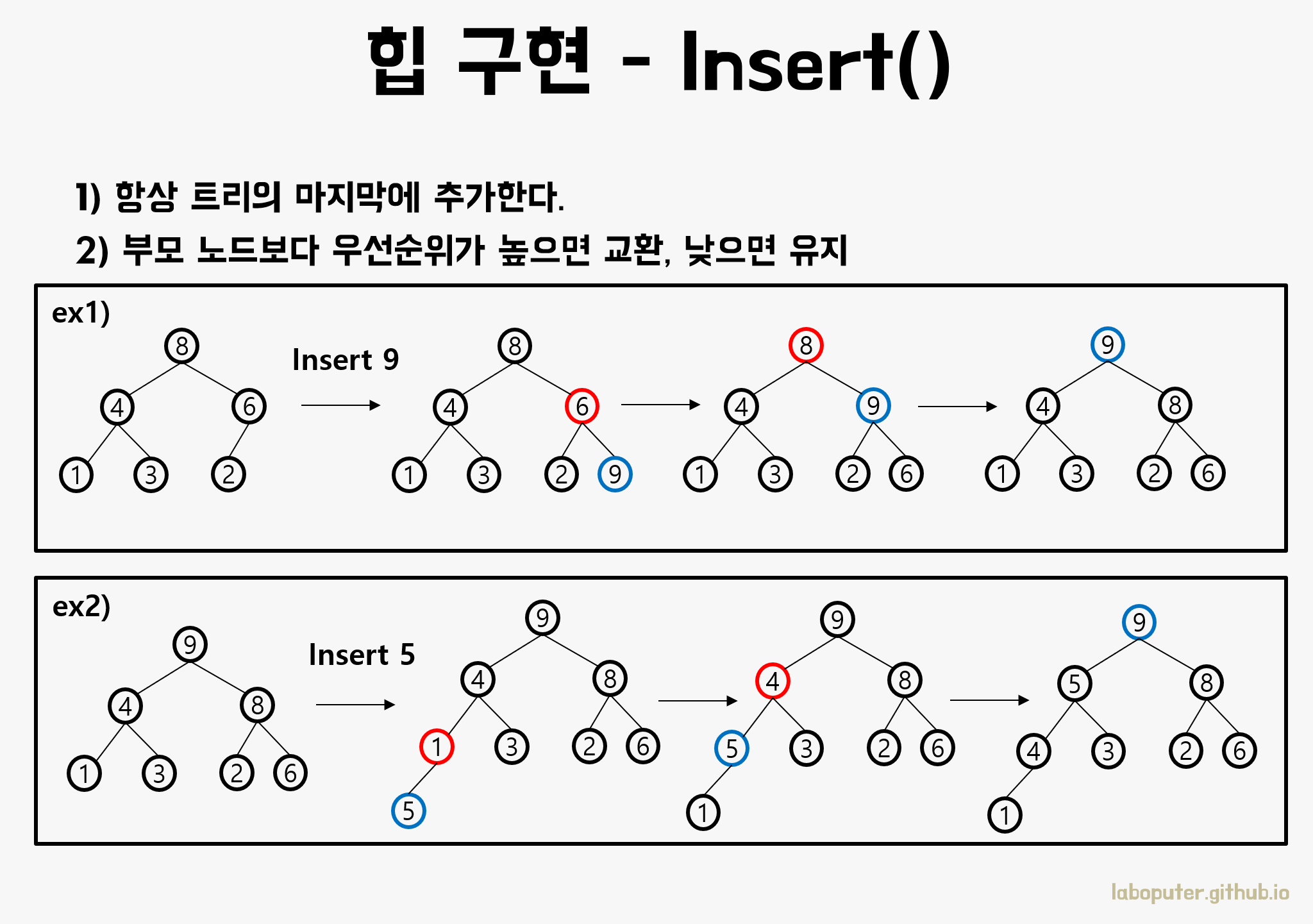
추가(Insert) 연산
- 항상 트리의 마지막에 데이터를 추가한다.
- 추가한 데이터가 부모 노드보다 우선순위가 높으면 교환한다.
- 루트이거나 부모 노드보다 낮을때까지 2를 반복한다.
위 순서에 따라 진행하면 데이터를 추가해도 항상 힙의 구조를 유지할 수 있습니다. 그림에서 나온 것처럼 2가지 예시를 보면서 이해하시면 됩니다.
시간복잡도를 생각해보면 힙은 완전이진트리 때문에 높이는 H = logN 이며, 최악의 경우 루트까지 교환하는 것이므로 O(logN) 입니다.
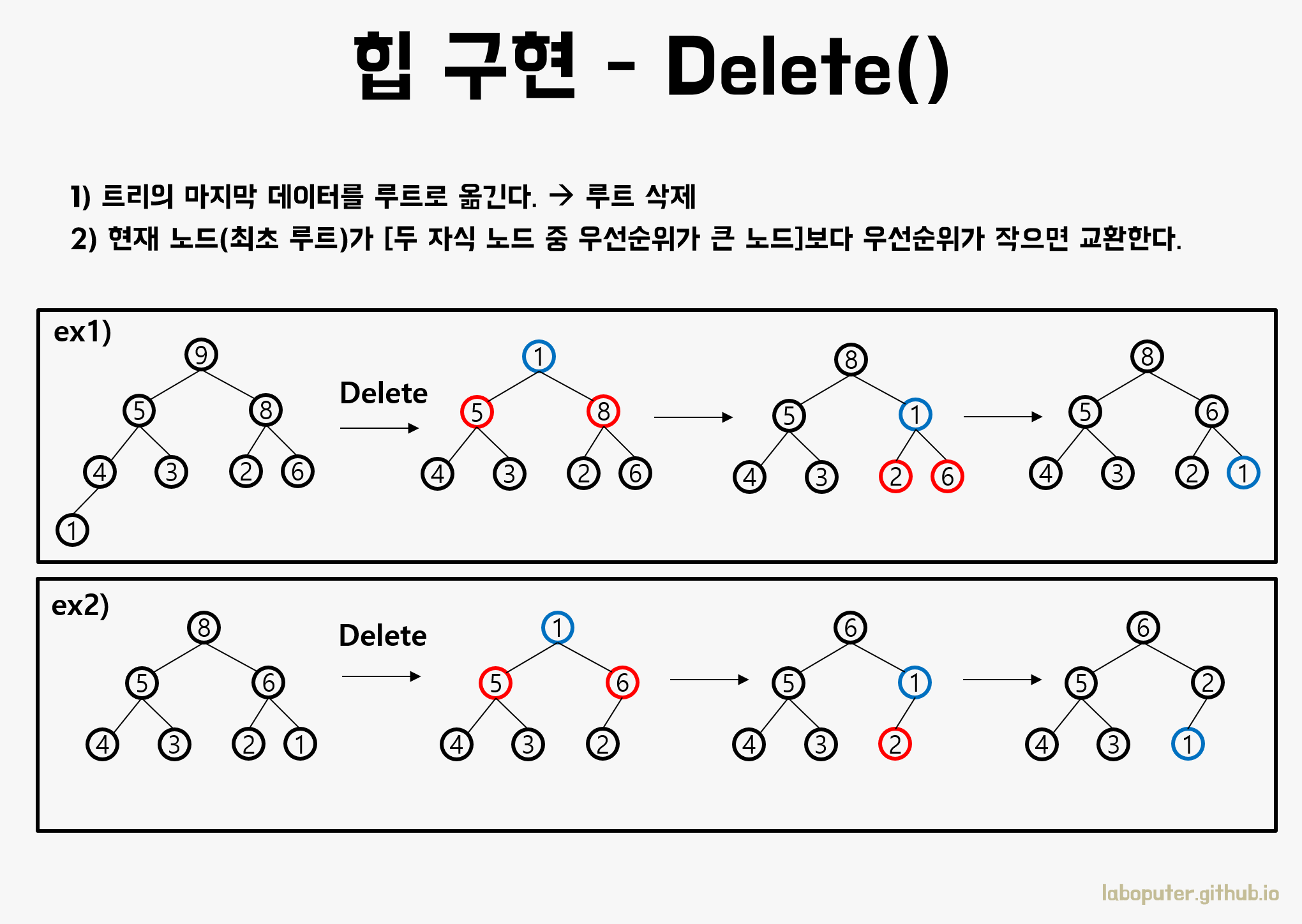
삭제(Delete) 연산
- 루트를 삭제하고 마지막 노드를 루트로 옮긴다.
- 두 자식노드 중 우선순위가 큰 노드보다 현재 노드가 우선순위가 작으면 교환한다.
- 현재노드가 우선순위가 가장 클 때 까지 2를 반복한다.
마찬가지로 위 순서에 따라 진행하면 데이터를 삭제해도 항상 힙의 구조를 유지할 수 있습니다.
역시 시간복잡도를 생각해보면 가장 우선순위가 높은 데이터를 확인하는 것은 O(1)이고, 삭제 연산은 추가 연산과 마찬가지로 최대 높이만큼 동작하기 때문에 O(logN)이 됩니다.
실제 구현 코드는 예제 풀이를 확인하세요.
예제: 최대힙
문제 링크:: 최대힙(https://www.acmicpc.net/problem/11279)
자세한 문제 설명은 위 링크로 들어가셔서 확인하시고 직접 풀어보세요!
힙을 구현하는 기본 문제로 최대힙은 큰 수가 우선순위가 높은 힙입니다. 무작위로 추가 연산을 해야 하고, 삭제 연산도 수행하면서 여태까지 저장된 가장 큰 값을 출력해야 합니다.
풀이
문제의 제약조건을 보면 최대 10만번의 추가 또는 삭제 연산이 주어집니다. 그렇기 때문에 각 연산의 시간 복잡도가 O(logN) 이하로 수행되어야 하고 문제에 따라 삭제 연산을 수행할 때 최대값을 알아야 하기 때문에 힙으로 쉽게 풀 수 있습니다.
전체 코드:
#include <stdio.h>
#define MAXN 100005
struct heap
{
int a[MAXN];
int sz = 0;
void swap(int i, int j)
{
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
void PUSH(int x)
{
sz++;
a[sz] = x;
if (sz == 1) return;
int cur = sz;
int p = sz / 2;
while (p && a[p] < a[cur])
swap(p, cur), p /= 2, cur /= 2;
}
void POP()
{
a[1] = a[sz];
sz--;
int cur = 1;
int l = 2;
int r = 3;
while (l <= sz)
{
if (r <= sz && a[l] < a[r] && a[cur] < a[r])
swap(cur, r), cur = r;
else if (l <= sz && a[cur] < a[l])
swap(cur, l), cur = l;
else
break;
l = cur * 2;
r = cur * 2 + 1;
}
}
int TOP()
{
return a[1];
}
};
int main(void)
{
int N; scanf("%d", &N);
heap pq;
for (int i = 0, x; i < N; i++)
{
scanf("%d", &x);
if (x != 0)
pq.PUSH(x);
else
{
if (pq.sz == 0)
printf("0\n");
else
{
printf("%d\n", pq.TOP());
pq.POP();
}
}
}
return 0;
}
우선순위 큐가 이미 구현되어 있는 C++의 priority_queue<>을 사용할수 있습니다.
priority_queue<>를 이용한 코드:
#include <stdio.h>
#include <queue>
using namespace std;
#define MAXN 100005
int main(void)
{
int N; scanf("%d", &N);
priority_queue<int> pq;
for (int i = 0, x; i < N; i++)
{
scanf("%d", &x);
if (x != 0)
pq.push(x);
else
{
if (pq.size() == 0)
printf("0\n");
else
{
printf("%d\n", pq.top());
pq.pop();
}
}
}
return 0;
}
다른 문제 추천
- 가운데를 말해요: (https://www.acmicpc.net/problem/1655)
- 카드 정렬하기: (https://www.acmicpc.net/problem/1715)
우선순위 큐도 대부분의 언어에서 STL이 있지만 알고리즘을 배우는데 있어 중요하다고 생각하여 직접 구현해보았습니다. 이미 구현하실 수 있으시면 안정적인 STL을 사용하세요!