[자료구조 2] 서로소 집합(Disjoint Set) 이해하기
데이터들을 여러가지 집합으로 분류해주는 연산이 빠른 자료구조로
서로소 집합(Disjoint Set)을 사용할 수 있습니다. 이는유니온파인드(Union-Find)라고 부르기도 합니다. 이 포스팅에서는 서로소 집합이 특징이 무엇이고, 어떻게 구현하는지를 예제를 통해 알아봅니다.
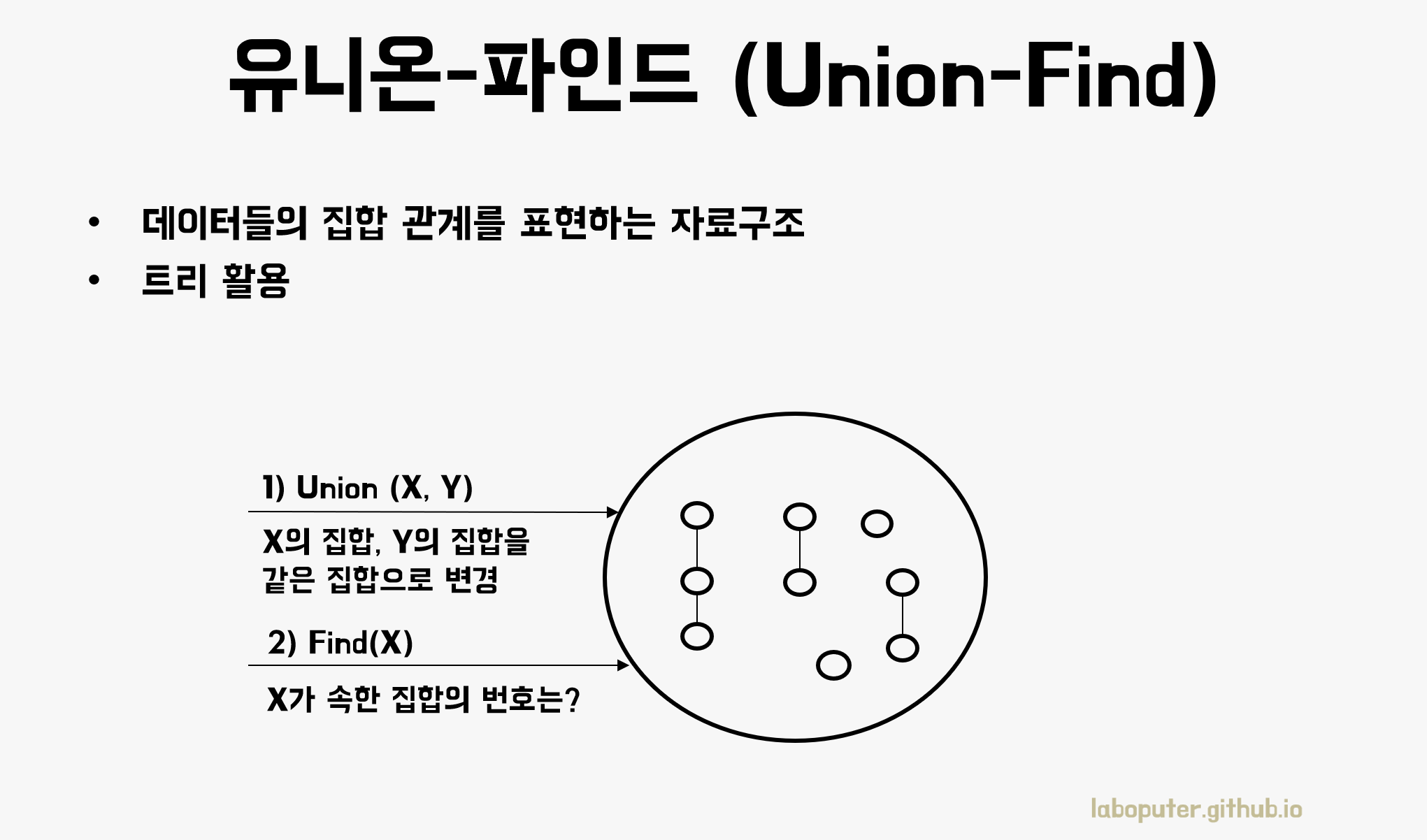
서로소 집합(Disjoint Set)
서로소 집합은 집합 관계를 표현할 수 있는 자료구조입니다. 같거나 다른 집합으로 분리해줄 뿐만 아니라 최대 N개의 집합으로 분리할 수도 있습니다.
서로소 집합은 2가지 연산이 있습니다.
- Union(X,Y): X가 속한 집합과 Y가 속한 집합을 합친다.
- Find(X): X가 속한 집합의 대표번호를 반환한다.
그래서 유니온파인드(Union-Find)로도 부르기도 합니다. 앞으로는 기억하기 쉽게 유니온파인드로 부르겠습니다.
시간복잡도
일반적인 배열로 접근하면 Union 연산은 대표 번호로 최대 N개의 수를 변경해야하기 때문에 O(N)이고, Find 연산은 대표번호를 바로 알 수 있기 때문에 O(1)입니다.
유니온파인드는 트리로 구현하면 Union 연산은 Find 연산을 이용하여 구현할 수 있고, Find 연산은 최악의 경우 O(N)이지만, 몇 가지 트릭으로 O(a(N))으로 만들 수 있습니다. 이는 O(1)로 취급해도 될 정도로 빠릅니다.
a(N)은 아커만 함수로 아주 큰 수도 4 이하가 되는 함수라고 하네요.
따라서 유니온파인드의 시간복잡도는 다음과 같습니다.
- Find: O(a(N)) => O(1)
- Union: O(a(N)) => O(1)
유니온-파인드 구현
유니온파인드는 트리를 이용합니다. 그 이유는 트리의 루트를 각 집합의 대표번호로 표현하면 서로 다른 집합이면 트리가 분리되어 있는데, 이를 같은 집합으로 만드려면 트리를 붙여주기만 하면 되기 때문입니다.
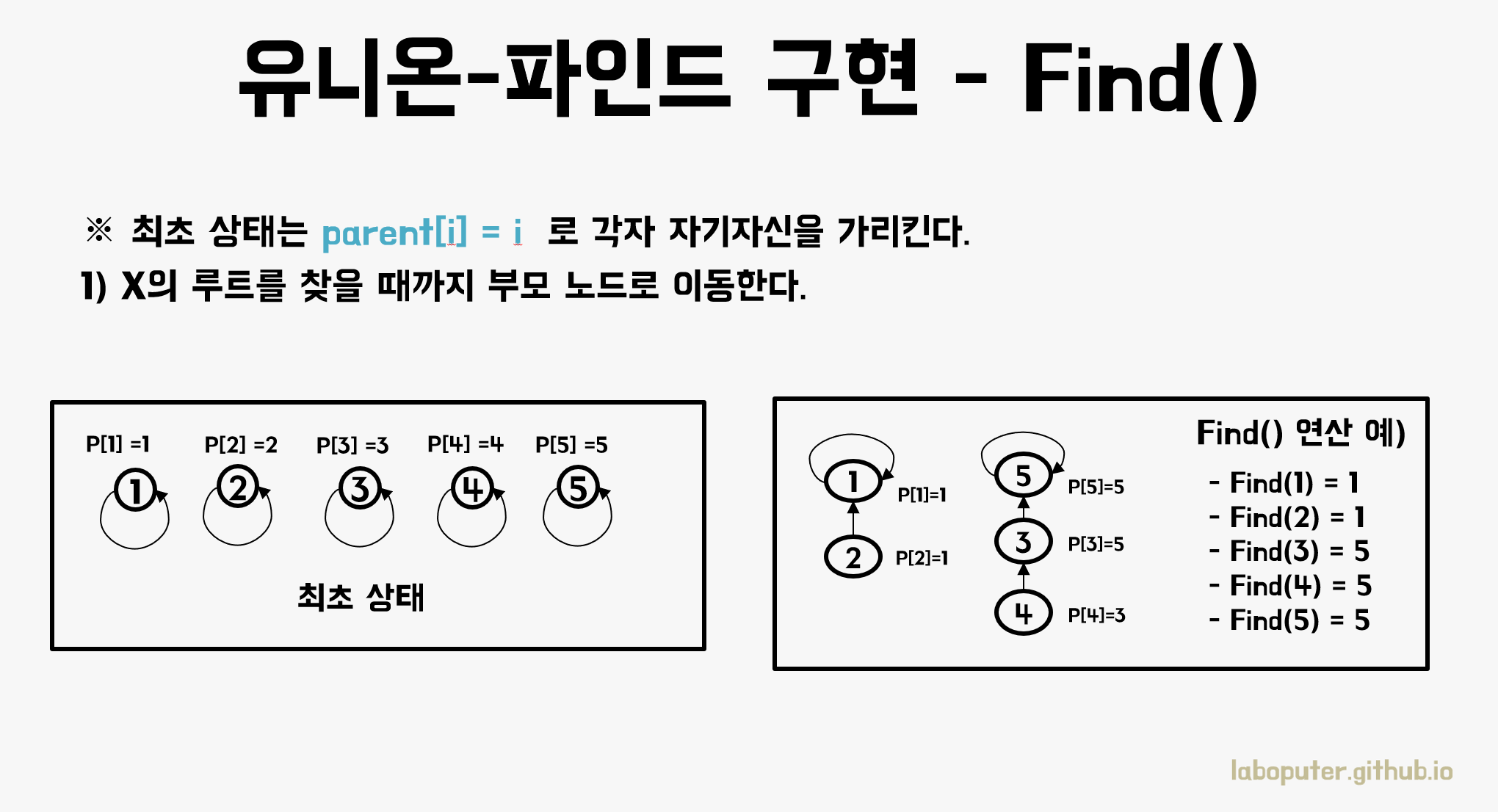
Find 연산
parent[i]라는 부모의 노드번호를 저장한 트리를 사용합니다. 최초 상태는 자기 자신을 가리키게 됩니다.
Find 연산은 루트를 찾는 것이기 때문에 parent[i] == i가 같을 때까지 부모 노드로 이동하기만 하면 됩니다.
아래 코드처럼 구현하면 됩니다.
int parent[MAXN];
for (int i = 0; i < MAXN; i++)
parent[i] = i;
int Find(int x)
{
return parent[x] == x ? x : Find(parent[x]);
}
여기서 시간복잡도는 최악의 경우 트리가 선형적으로 구성될 수 있기 때문에 O(N) 입니다.
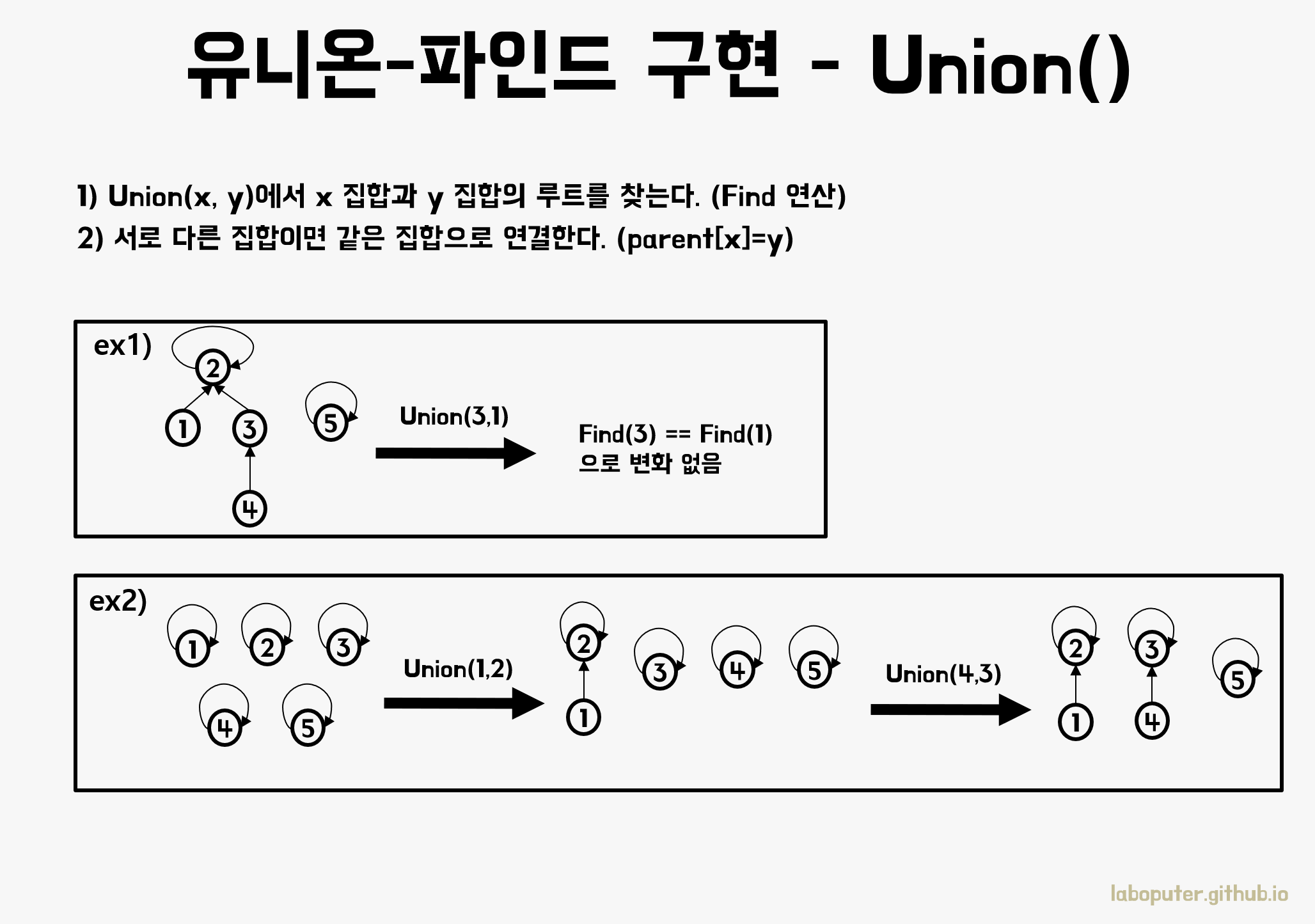
Union 연산
Union 연산은 Find 연산으로 쉽게 구현할 수 있습니다.
- X와 Y의 루트를 Find 연산으로 구한다.
- 서로 다른 집합인 경우, 같은 집합으로 만든다.
위 그림에서 1번째 예를 보면 이미 3과 1은 루트가 2로 같은 집합입니다. 2번째 예를 보면 다른 집합이면 트리의 루트를 다른 하나의 루트값으로 변경하면 됩니다.
구현 코드는 아래와 같습니다.
void Union(int x, int y)
{
parent[Find(x)] = Find(y);
}
두 가지 연산 모두 구현은 쉽지만 중요한 것은 어떻게 최적화할 것인가입니다.
Union-Find 최적화
최적화는 총 2가지 트릭을 통해 Union, Find 연산을 O(1)에 가깝게 만들어줍니다.
첫번째는 경로 압축(Path Compression) 입니다.
Find 연산을 재귀적으로 실행할 때 한번 찾은 부모값을 계속 갱신해놓는 것입니다. 그러면 다음 번에 같은 노드의 부모를 찾아야할 때 바로 찾을 수 있게 됩니다.
int Find(int x)
{
// return (parent[x] == x ? x : Find(parent[x]));
// path compression
return parent[x] = (parent[x] == x ? x : Find(parent[x]));
}
사실 위 한가지 트릭만 적용해도 유니온파인드는 충분히 빠릅니다.
두번째는 랭크를 통한 합치기(Union by Rank) 입니다.
Union 연산에서 트리를 합칠 때 한쪽으로만 합치는 것이 아니라 트리의 높이가 낮은 것을 트리의 높이가 높은 곳으로 합치는 것입니다. 그래야 높이가 최소화되기 때문입니다.
각 트리의 높이를 저장한 rank 값은 트리의 높이가 다를 때는 높은쪽으로 낮은 것이 붙기 때문에 그대로 일 것이고, 트리의 높이가 같아지면 반드시 높이가 증가하기 때문에 +1 이 될 것입니다.
void Union(int x, int b)
{
x = Find(x), y = Find(y);
if (x==y) return;
// union by rank
if (rank[x] > rank[y]) swap(x, y);
parent[x] = y;
if (rank[x] == rank[y]) rank[y]++;
}
예제: 집합의 표현
문제 링크:: 집합의 표현(https://www.acmicpc.net/problem/17219)
자세한 문제 설명은 위 링크로 들어가셔서 확인하시고 직접 풀어보세요!
이 문제는 유니온 파인드 연산을 그대로 구현하는 기본 문제입니다.
풀이
문제의 제약조건에서 m은 10만까지 가능하기 때문에 Union과 Find를 각각 O(logN) 이하로 해결해야 합니다.
유니온파인드 자료구조를 구현하면 가능합니다.
전체 코드:
#include <stdio.h>
#define MAXN 1000005
struct UF
{
int parent[MAXN];
int rank[MAXN];
UF()
{
for (int i = 0; i < MAXN; i++) parent[i] = i;
}
int Find(int x)
{
// path compression
return parent[x] = (parent[x] == x ? x : Find(parent[x]));
}
void Union(int a, int b)
{
a = Find(a), b = Find(b);
if (a==b) return;
// union by rank
if (rank[a] > rank[b]) swap(a, b);
parent[a] = b;
if(rank[a] == rank[b]) rank[b]++;
}
void swap(int a, int b)
{
int tmp = a;
a = b;
b = tmp;
}
};
int N, M;
int main()
{
scanf("%d%d", &N, &M);
UF uf;
for (int i = 0, x, a, b; i < M; i++)
{
scanf("%d%d%d", &x, &a, &b);
if (x == 0) uf.Union(a, b);
else printf("%s\n", (uf.Find(a) == uf.Find(b) ? "YES" : "NO"));
}
return 0;
}
다른 문제 추천
- 친구 네트워크: (https://www.acmicpc.net/problem/4195)
- Count Circle Groups: (https://www.acmicpc.net/problem/10216)
알고리즘 문제에서 간혹 등장하지만 일반적인 프로그래밍에서는 필요를 느낀적은 많이 없었습니다. 그래서인지 STL을 지원하지 않는 언어가 많아 필요하면 직접 구현할 수 있어야 합니다. 그래도 한번 이해하면 어렵지 않게 구현하실 수 있습니다.