추가와 삭제, 거기다 검색까지 빠른 자료구조인 이진검색트리(Binary Search Tree)에 대해 알아보고자 합니다. 이 포스팅에서는 이진검색트리가 무엇이고, 어떻게 구현해야 하는지를 다룹니다.

이진검색트리(Binary Search Tree)

그동안 검색이 빠른 자료구조들을 여러 포스팅에서 다뤘습니다. 배열은 논외로 하고 해시테이블과 힙이 대표적입니다. 힙은 추가/삭제/검색이 O(logN) 으로 빠르지만 가장 큰값, 작은값처럼 우선순위가 가장 높은 것만 찾을 수 있는 반면, 이진 검색트리는 모든 값을 빠르게 탐색할 수 있습니다.

그리고 해시테이블도 추가/삭제/검색이 빠르지만 데이터가 몇개인지에 따라 해시테이블의 메모리 크기와 해시키값이 고려되어야 합니다.

하지만 이진검색트리(Binary Search Tree)는 그런 제약들이 없이 추가/삭제/검색이 모두 빠른 자료구조입니다.

이진 검색트리는 현재 노드를 기준으로 데이터가 작은 노드는 왼쪽에, 큰 노드는 오른쪽에 위치하도록 트리를 유지한 구조입니다. 추가/삭제 연산을 해도 이 구조를 유지하는 것이 관건입니다. 그렇게 되면 효율적인 탐색이 가능합니다.

시간복잡도

현재 노드를 기준으로 왼쪽 서브트리는 작은 노드들이, 오른쪽 서브트리는 큰 노드들이 위치해 있는 특성에 따라 특정한 값을 검색하면 최악의 경우에도 높이 H 만큼 탐색하므로 O(H) 입니다.

추가/삭제 연산도 구현하면서 이해되시겠지만 최대 높이 H 만큼 확인하면 되기 때문에 O(H) 입니다.

높이에 따라 모든 연산의 효율이 결정되므로 우리는 이진검색트리의 높이를 H = logN 에 가깝게 만들 것입니다. 실제로 그렇게 할 수 있습니다.

따라서 이진검색트리의 시간복잡도는 다음과 같습니다.

• 추가(Insert): O(logN)
• 삭제(Delete): O(logN)
• 검색(Search): O(logN)

이진검색트리의 구현

여기에서의 구현은 트리의 높이에 신경쓰지 않고 이진검색트리의 특성인 모든 노드에서 왼쪽 서브트리는 작고, 오른쪽 서브트리는 큰 구조가 만족하게 하는 것이 목표입니다.

검색(Search) 연산

원하는 데이터가 있는지 탐색하는 것은 특성을 이해하시면 쉽습니다. 루트부터 시작해서 확인해보고 더 작은 노드를 찾아야 하면 왼쪽으로, 더 큰 노드를 찾아야 하면 오른쪽으로 가면 됩니다. 원하는 것을 찾을 때 까지 반복하고 만약 빈공간을 만나면 원하는 데이터가 없는 것입니다.

그렇기 때문에 트리의 높이만큼 탐색만 해보면 됩니다. 따라서 시간복잡도는 O(H) 입니다.

추가(Insert) 연산

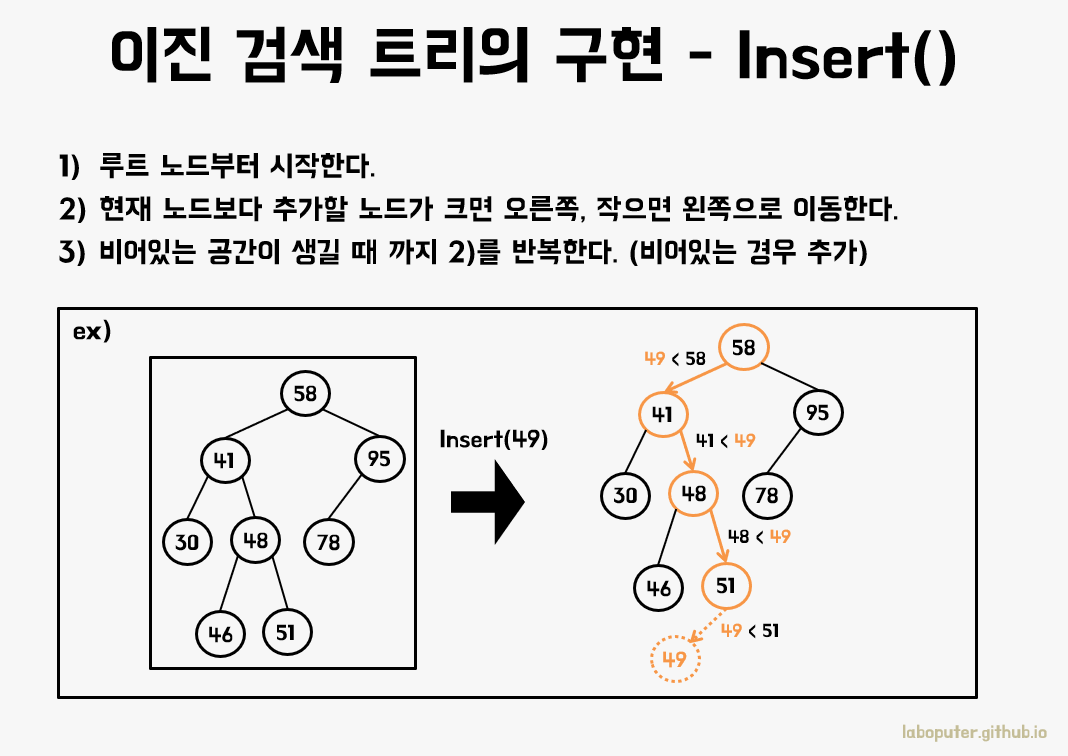
데이터를 추가하는 것도 검색와 유사합니다. 루트부터 시작해서 현재 노드가 작으면 왼쪽으로, 크면 오른쪽으로 계속 이동하기만 하면 됩니다. 그러다가 빈공간이 나오면 그 자리에 추가해주면 끝입니다.

그림의 예시처럼 49를 추가하기 위해서 루트부터 확인해서 값이 크고 작음에 따라 이동하다가 빈공간에 추가하면 됩니다.

마찬가지로 트리의 높이만큼만 확인하면 추가할 수 있으므로 O(H) 입니다.

삭제(Delete) 연산

삭제를 하기 위해서는 삭제할 데이터를 검색해야 합니다. 찾았다면 삭제를 진행하는데 이 때 삭제할 노드의 자식 노드가 몇 개인지에 따라 조금 다릅니다.

우선 자식 노드가 없으면 그냥 삭제해도 구조가 유지됩니다. 자식 노드가 1개일 때는 현재 노드만 삭제하고 자식을 루트로 하는 서브트리를 그냥 연결만 해주면 됩니다. 그 이유는 이미 삭제할 노드의 서브트리가 특성을 만족하고 있었기 때문입니다.

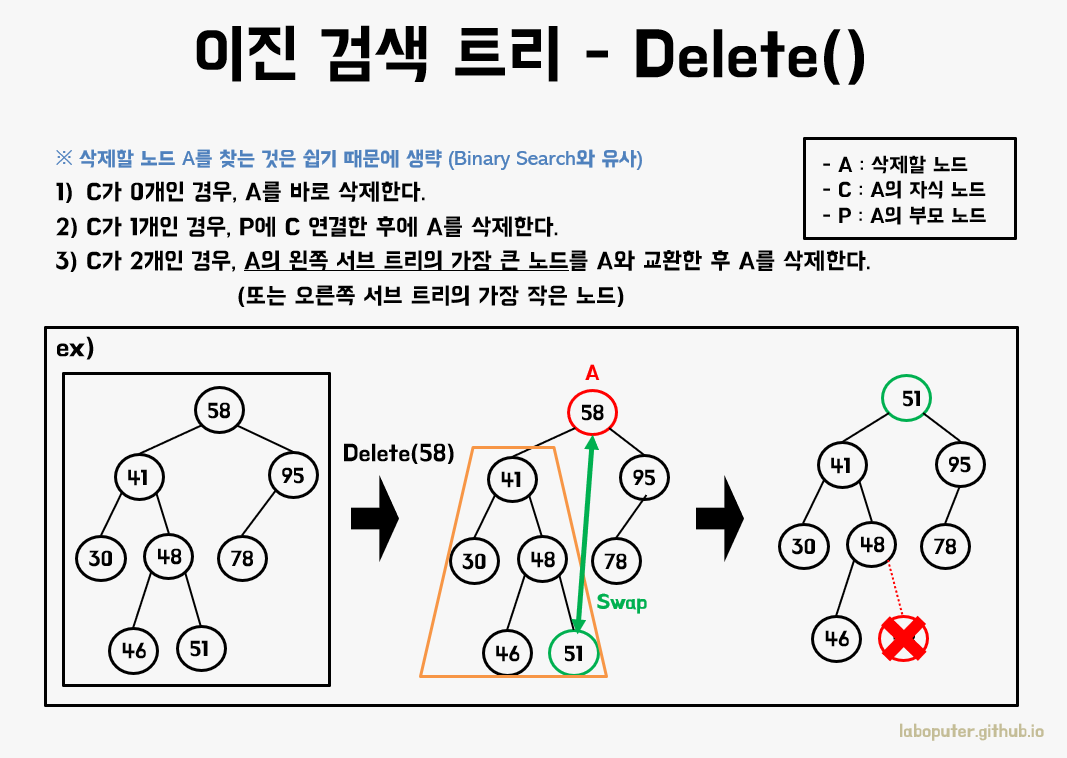
자식 노드가 2개인 경우는 삭제할 노드를 기준으로 왼쪽에 있을 값, 오른쪽에 있을 값이 모두 있기 때문에 삭제할 노드의 위치를 대신할 노드가 필요합니다. 그것은 왼쪽 서브트리의 가장 큰 값 또는 오른쪽 서브트리의 가장 작은 값임을 알 수 있습니다.

그림의 예시를 통해 더 자세히 설명하면 58을 삭제하려고 할 때 58의 위치를 어떤 노드가 대신 해야 구조가 유지될 지를 고민하면 됩니다. 58보다 아주 조금 작거나, 아주 조금 크면 됩니다. 그래야 원래 구조와 최대한 비슷하니까요. 58보다 아주 조금 작다는 것은 왼쪽 서브트리에서 가장 큰 값이고, 아주 조금 크다는 것은 오른쪽 서브트리에서 가장 작은 값입니다. 우리는 둘 중 하나를 선택하면 됩니다.

따라서 그림의 예처럼 왼쪽 서브트리의 가장 큰 값을 찾아 삭제할 노드로 옮긴 후에 삭제하면 됩니다.

삭제 연산의 시간복잡도를 생각해보면 자식 노드가 0 또는 1개이면 O(1), 자식 노드가 2개면 왼쪽 서브트리의 가장 큰 값을 찾는 연산 O(H)이고 공통적으로 삭제할 데이터를 찾는 연산 O(H) 이므로 최종적인 시간복잡도는 O(H) 입니다.

그러면 이제 높이 H를 logN에 가깝게 이진검색트리를 만들지를 고민해봐야 합니다.

균형잡힌 이진검색트리(Balanced BST)

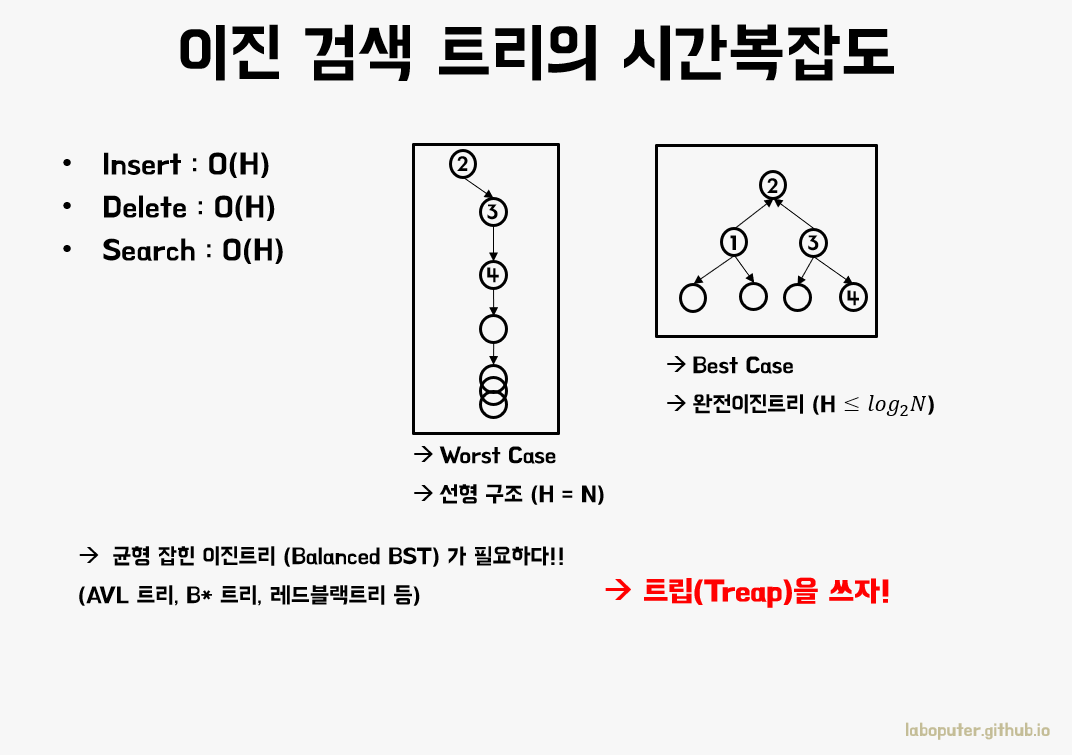
모든 연산의 시간복잡도가 높이 H에 영향을 받습니다. 하지만 최악의 경우 이진검색트리가 일렬로(Skewed) 구성될 수 있습니다.

그림의 Worst Case처럼 2,3,4,5,.. 처럼 오름차순으로 정렬된 데이터가 순서대로 추가되면 나타납니다. 우리는 데이터가 어떤 순서로 들어오든 작은 logN로 이진검색트리를 만들어야 합니다. 우리는 이것을 통틀어 균형잡힌 이진검색트리(Balanced BST)라고 부릅니다.

이러한 균형잡힌 이진검색트리는 AVL트리,B* 트리, 레드블랙트리 등 많이 있습니다.

하지만 구현 자체가 너무 길어서 전공수업때나 구현해보는 것이 좋고, Problem Solving을 연습할 때는 비슷한 효과를 내면서 구현이 쉬운 자료구조를 사용합니다.

종만북 저자분의 조언대로 트립(Treap)이라는 자료구조를 사용하는 것이 좋겠습니다.

트립은 포스팅이 준비되면 올리겠습니다.

이 포스팅에서 다룬 시간복잡도가 O(H)인 이진검색트리로는 예제를 풀만한 것이 없기 때문에 생략하겠습니다.