[알고리즘 설계] 2. 분할정복(Divide and Conquer)
in Problem Solving on Algorithm
분할정복은 어떤 문제를 풀기 위해 문제를 작게 나눠 푸는 방법입니다. 이 기법을 이해하기 위해 여러가지 예제를 통해 설명하고 연습문제를 풀면서 직접 구현해보는 것이 목표입니다.
분할정복 (Divide and Conquer)
분할정복(Divide and Conquer)은 말그대로 어떤 문제를 작은 문제로 분할(Divide)하여 풀고 이 부분 문제의 해를 통해 전체 문제의 해를 구하는 것(Conquer)을 말합니다.
어떤 문제든 작은 문제(N이 작은)는 풀기가 아주 쉽습니다. 정렬 문제로 예를 들면 데이터가 2개면 크고 작은지 비교하고 위치만 변경하면 되고, 데이터가 1개면 이미 문제를 푼 것입니다.
이렇게 풀기 쉬운 작은 문제의 결과를 조합하면 전체 문제의 해를 훨씬 빠른 시간안에 구할 수 있습니다. 물론 모든 문제에 적용될 수는 없지만 어떤 문제들은 작은 문제를 해결하여 구하는 것이 시간복잡도를 줄여주는 경우가 있습니다.
분할정복 알고리즘
- 문제를 둘 이상의 부분문제로 나눈다.
- 바로 해결가능한 아주 작은 부분 문제는 즉시 결과를 구한다. (N=0 또는 1 등)
- 각 부분문제의 답을 이용하여 전체 문제의 답을 구한다.
위 방법을 보시면 아시겠지만 전체 문제의 답을 구하기 위해 부분 문제의 답을 구하는 구조로 재귀를 이용합니다. 그리고 2번에서 설명하는 것은 재귀에서의 기저(Base)를 말합니다.
여기서 분할정복이 의미있으려면(시간복잡도가 줄어들려면) 부분문제의 해를 이용하여 전체문제의 해를 구할 때는 반드시 효율적인 방법이 있어야 합니다. 이 내용은 예제로 감을 잡아봅시다.
분할정복 사고연습
예제1. 3^N 의 결과값은?
(단, N은 자연수이고, N <= 1000)
이 문제는 N 값이 커짐에 따라 오버플로우가 발생하지만 설명과 무관하므로 무시합니다.
완전탐색 접근:
3을 N번 곱하는 것으로 쉽게 구할 수 있습니다. 시간복잡도는 O(N) 입니다.
분할정복 접근:
분할정복을 이용하면 훨씬 빠르게 구할 수 있습니다.
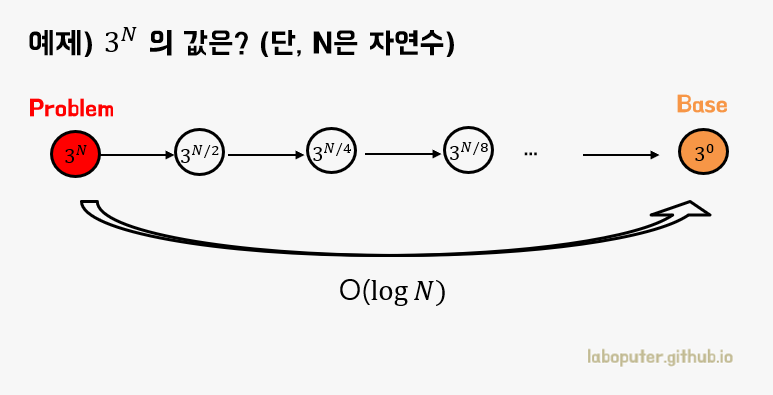
그림에서 빨간색 원인 3^N을 구하기 위해서는 3^(N/2)인 부분문제 둘로 나눌 수 있습니다. 이렇게 나누는 작업을 계속 반복하면 3^0 = 1 로 해를 바로 구할 수 있는 Base를 만나게 됩니다. 또한 3^N은 3^(N/2) 문제의 해만 구하면 제곱하기만 하면 되기 때문에 쉽게 구할 수 있습니다.
시간복잡도를 생각해보면 부분문제의 해(3^(N/2))를 이용하여 전체 문제의 해를 구하는 것은 O(1) 이고 부분문제를 나누는 깊이는 logN 이기 때문에 전체 시간복잡도는 O(logN) 입니다.
예제2. N개의 수 정렬하기(오름차순)
완전탐색 접근:
가장 작은 수를 찾고 0번째 인덱스의 데이터와 교환합니다. 그리고 1 ~ N-1 번째 데이터에서 또 가장 작은수를 찾고 1번째 인덱스와 교환합니다. 이를 반복하면 끝입니다. 이렇게 정렬하는 방법을 선택정렬(Selection Sort)이라고 하고 시간복잡도는 O(N^2) 입니다.
분할정복 접근:
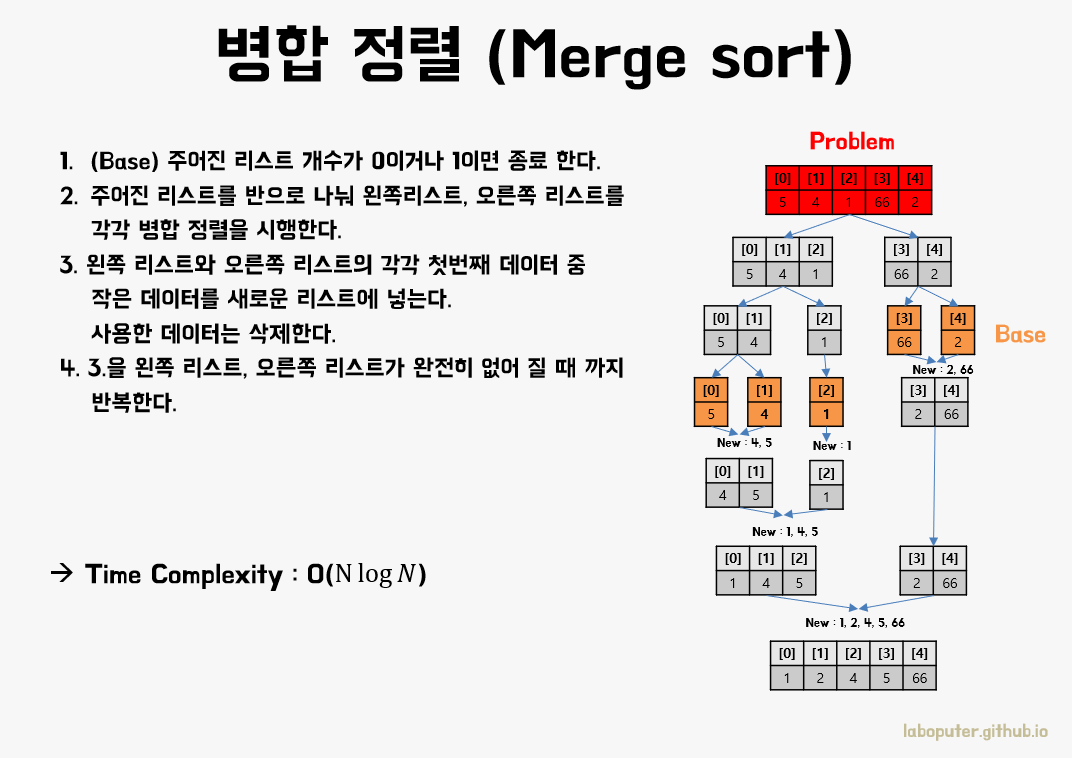
그림에서처럼 N개의 데이터를 반씩 둘로 나눕니다. 마찬가지로 나누는 작업을 반복하면 바로 해를 구할 수 있는 N=1인 Base 까지 나눠집니다. 또한 데이터가 반반씩 각각 정렬된 데이터(부분문제의 해)가 있으면 전체문제를 정렬하는 효율적인 방법은 왼쪽리스트와 오른쪽리스트의 첫번째 데이터끼리 확인해서 작은 숫자를 가져오는 방식으로 모든 데이터를 한번만 보면 됩니다.
그림에서 정렬되는 과정을 보면 재귀함수를 통해 데이터들이 모두 분할(Divide)된 이후에 Base를 만나면 나눠졌던 문제들이 해결되면서 합쳐지는 것을 보실 수 있습니다. 이와 같이 분할정복으로 데이터를 정렬하는 것을 병합 정렬(Merge sort)이라고 합니다.
따라서 시간복잡도는 부분문제의 해(왼쪽 데이터 정렬, 오른쪽 데이터 정렬)를 이용하여 전체 문제의 해(전체 데이터 정렬)를 구하는 것은 O(N) 이고, 부분문제가 나뉘어지는 깊이는 logN 이기 때문에 O(NlogN) 입니다.
연습문제
문제 링크:: 수 정렬하기 2(https://www.acmicpc.net/problem/1182)
자세한 문제 설명은 위 링크로 들어가셔서 확인하시고 직접 풀어보세요!
분할정복에서 기본적인 문제로 위에서 ‘예제2’로 다룬 수 정렬하기 문제입니다. 분할정복을 이해하는 것이 목적이니 라이브러리는 사용하지 않고 직접 구현해보시길 바랍니다.
풀이
N의 제약은 100만 이므로 버블정렬, 선택정렬과 같이 O(N^2) 방법은 시간초과로 풀 수 없습니다. 따라서 이 포스팅에서 배운 분할정복 기법을 이용한 병합정렬로 구현하시면 됩니다.
병합정렬은 시간복잡도가 O(NlogN) 이기 때문에 무난하게 통과하실 것입니다.
전체 코드:
#include <stdio.h>
#define MAXN 1000005
int N;
int arr[MAXN];
int tmp[MAXN];
void MergeSort(int l, int r)
{
if (l >= r) return;
int m = (l + r) >> 1;
MergeSort(l, m);
MergeSort(m + 1, r);
int p1 = l, p2 = m + 1, p3 = l;
while (p1 <= m && p2 <= r)
tmp[p3++] = (arr[p1] < arr[p2]) ? arr[p1++] : arr[p2++];
while (p1 <= m)
tmp[p3++] = arr[p1++];
while (p2 <= r)
tmp[p3++] = arr[p2++];
for (int i = l; i <= r; i++)
arr[i] = tmp[i];
}
int main()
{
scanf("%d", &N);
for (int i = 0; i < N; i++)
scanf("%d", &arr[i]);
MergeSort(0, N - 1);
for (int i = 0; i < N; i++)
printf("%d\n", arr[i]);
return 0;
}
위와 같이 재귀함수로 간단하게 분할정복을 이용한 정렬을 하실 수 있습니다.
다른 연습문제 추천
- 하노이 탑 이동 순서: (https://www.acmicpc.net/problem/11729)
- 히스토그램에서 가장 큰 직사각형: (https://www.acmicpc.net/problem/6549)
분할정복은 특정한 상황에 효율적인 방법이므로 적용 방식에 대해 이해하셨다가 문제 푸실 때 비슷한 상황에서 접근해볼만한 알고리즘입니다.