[알고리즘 설계] 3. 동적계획법(Dynamic Programming)
in Problem Solving on Algorithm
동적계획법은 분할정복처럼 어떤 문제를 풀 때 부분문제의 해를 이용하여 구하는 것을 말합니다. 동적계획법을 이해하기 위해 여러가지 예제를 통해 설명하고 연습문제를 풀어보면서 직접 구현해보는 것이 목표입니다.
동적계획법 (Dynamic Programming)
동적계획법(Dynamic Programming)은 알고리즘 문제에서 정말 다양한 형태로 등장하기 때문에 이 방법으로 많은 문제를 해결할 수 있게 됩니다. 영어로는 Dynamic Programming 이라고 하지만 일반적인 프로그래밍에서 말하는 동적 프로그래밍 개념과는 전혀 관련이 없습니다.
동적계획법은 분할정복과 접근 방식이 비슷합니다. 어떤 문제를 작은 부분문제들로 나눠서 해결합니다. 다만 차이점은 문제를 어떻게 나누냐에 있습니다. 분할정복은 부분문제들을 한번만 구하면 되지만 동적계획법은 부분문제들이 여러번 사용되도록 문제를 분할합니다. 그래서 이미 해결한 부분문제들은 캐시 메모리에 넣어두고 이미 해결한 부분문제들의 해를 필요할 때는 메모리에 저장된 값을 사용합니다. 이렇게 메모리를 사용해 빠른 시간안에 구할 수 있도록 고안된 것입니다.
동적계획법이 효과적으로 동작하기 위해서 중요한 2가지 조건이 있습니다. 이 조건이 만족해야만 동적계획법을 적용하는 것이 의미있습니다.
동적계획법 적용조건
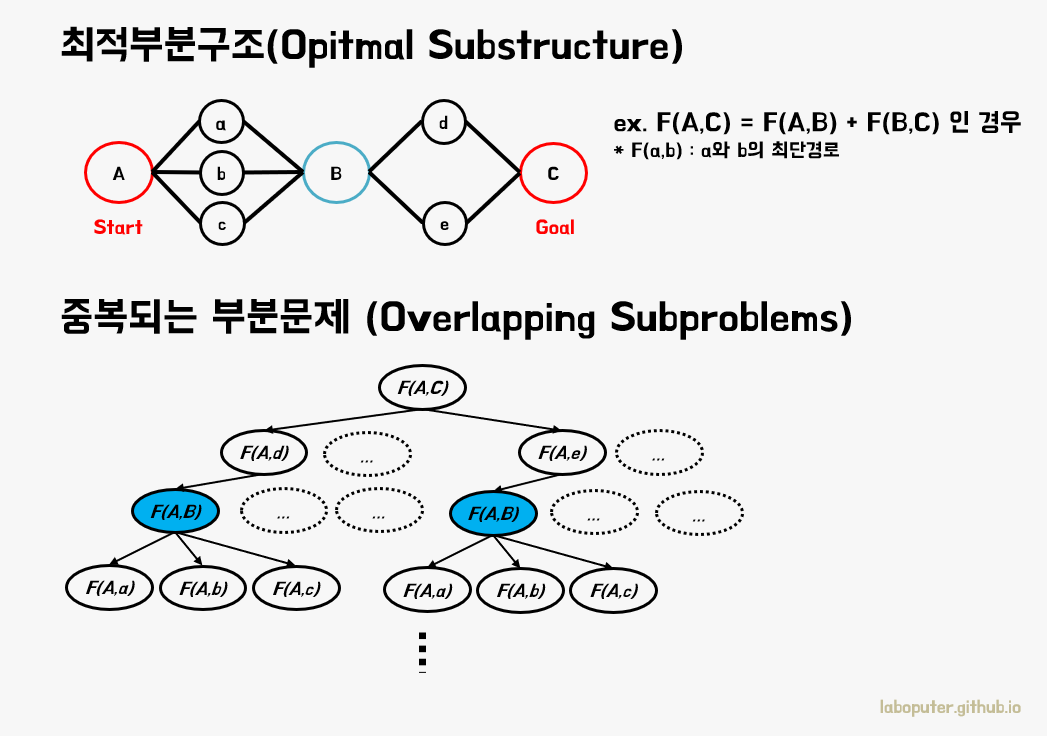
- 최적부분구조(Optimal Substructure)
- 전체문제의 해를 부분문제들의 해만으로도 구할 수 있게 분할가능한 구조
- 중복되는 부분문제(Overlapping Subproblems)
- 전체문제를 해결함에 있어 똑같은 부분문제가 중복되어 발생하는 문제
그림에서 첫번째 그래프가 주어졌을 때 A에서 C로 가는 최단경로를 구하려면 (A->B)의 최단경로와 (B->C)의 최단경로를 합하면 됩니다. 마찬가지로 전체 부분문제들에 대해서도 위와 같습니다. 이런 경우를 최적부분구조가 성립한다고 표현합니다.
하지만 통행료 만원 이하로 최단경로를 구하라는 문제로 바꾸면 (A->B)의 최단경로와 (B->C)의 최단경로에서 각각 어떤 도로를 이용해 통행료 얼마나 사용하느냐에 따라 최단경로가 달라질 수 있기 때문에 부분문제의 해들의 조합으로는 해를 구할 수 없습니다. 이런 경우에는 최적부분구조가 성립하지 않습니다.
중복되는 부분문제는 그림의 아래 그래프처럼 어떤 문제를 해결하기 위해 F(A,B)와 같은 똑같은 부분문제가 여러번 발생하는 경우를 말합니다.
이 두 가지 조건을 만족하면 다음과 같은 동적계획법 알고리즘을 이용할 수 있습니다.
동적계획법 알고리즘
- 전체문제의 해가 부분문제의 해를 포함하도록 문제를 분할한다.
- 부분문제의 해를 구한 후 메모리에 저장한다. (이미 구했다면 메모리의 값을 사용)
- 부분문제의 해를 이용해 전체문제의 해를 구한다.
이 알고리즘은 한번만 직접 구현해봐도 직관적으로 이해되실 것입니다. 다만 동적계획법을 적용가능한 조건은 반드시 숙지하고 있어야 문제에 적용가능한지 판단하는데 도움이 됩니다.
동적계획법 사고연습
예제1. 피보나치 수열의 N번째 수 F(N)은 ?
- 단, F(0) = 1, F(1) = 1 이고, (0 <= N <= 1000)
# 피보나치 수열 정의: F(N) = F(N-1) + F(N+2)
이 문제는 N이 커짐에 따라 오버플로우가 발생하지만 설명과 무관하므로 무시합니다.
완전탐색 접근:
피보나치 수열의 관계식을 있기 때문에 재귀로 쉽게 구현할 수 있습니다. 아래 코드처럼 구현하면 시간복잡도는 O(2^N) 이 됩니다.
int F(int n)
{
if(n == 0 || n == 1) return 1;
return F(n-1) + F(n-2);
}
동적계획법 접근:
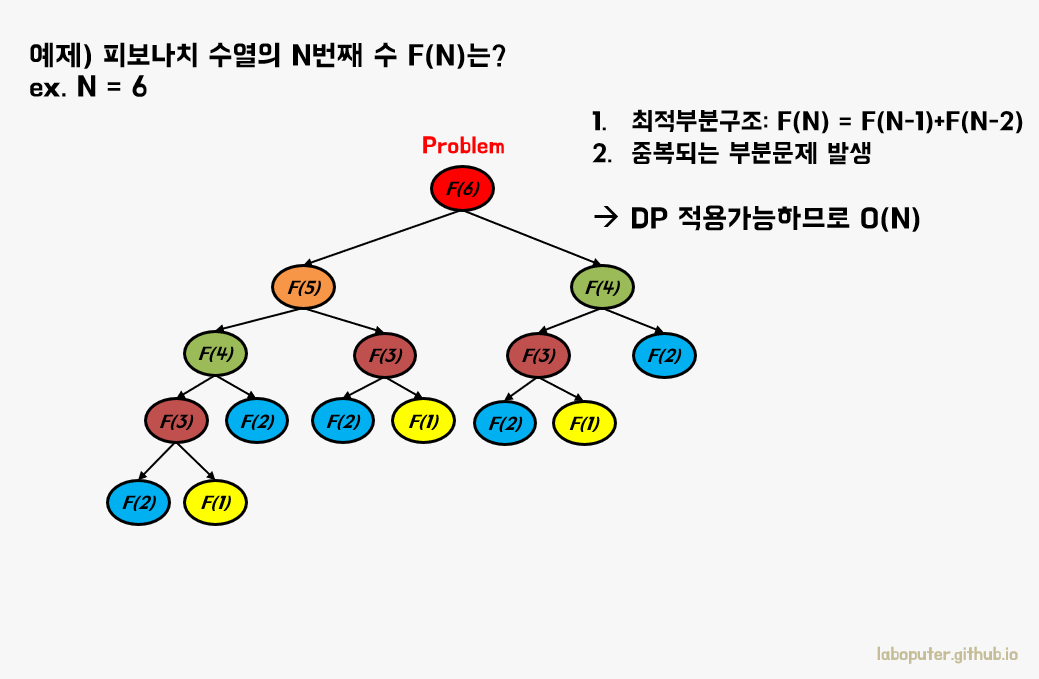
피보나치 수열의 정의에 따라 F(N) 을 구하기 위해서는 F(N-1) 와 F(N-2) 의 합으로 구할 수 있습니다. 다시 말하면 부분문제의 해만으로 전체문제의 해를 구할 수 있습니다. 즉 최적부분구조가 성립합니다.
위 그림처럼 F(6)을 구해야 한다면 모든 부분문제는 F(1) ~ F(6) 까지 6개의 해만 있으면 됩니다. 일반화하면 F(N)을 구하기 위해서는 N개의 부분문제에 대한 답만 있으면 모든 경우를 구할 수 있습니다. 재귀로 구할 때 똑같은 부분문제가 아주 많이 발생함을 알 수 있습니다. 즉 중복되는 부분문제가 성립함을 의미합니다.
그래서 동적계획법을 적용하면 시간복잡도는 부분문제를 알고 있을 때 모든 문제는 O(1) 로 구할 수 있고, 모든 부분문제의 종류는 N개 뿐이므로 전체 시간복잡도는 O(N) 이 됩니다.
코드를 보면 쉽게 이해되실 것입니다.
#define MAXN 1001
int f[MAXN];
f[0] = f[1] = 1;
for(int i=2; i<MAXN; i++)
{
f[i] = f[i-1] + f[i-2];
}
예제2: N, R 값이 주어질 때, 이항계수 nCr 값은 ?
단, (1 <= N <= 1000) 이고 (0 <= R <= N)
# 이항계수 관계식 : n C r = (n-1) C (r-1) + (n-1) C r
이 문제도 N, R 값이 커짐에 따라 오버플로우가 발생하지만 설명과 무관하므로 무시합니다.
이 문제도 동적계획법으로 접근하면 이항계수 관계식에 따라 최적부분구조가 성립하며, 재귀로 문제를 풀면 이항계수 부분 문제의 종류도 N*R 크기 안에서 중복되어 나타나기 때문에 중복되는 부분문제가 발생합니다.
따라서 동적계획법을 사용하면
#define MAXN 1005
int C[MAXN][MAXN];
for (int i = 0; i <= N; i++)
C[i][0] = C[i][i] = 1;
for (int i = 1; i <= N; i++)
for (int j = 1; j <= N; j++)
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
이렇게 모든 이항계수의 값을 구하는데 O(N^2) 로 가능합니다.
연습문제
문제 링크:: 가장 긴 증가하는 부분수열(https://www.acmicpc.net/roblem/11053)
자세한 문제 설명은 위 링크로 들어가셔서 확인하시고 직접 풀어보세요!
주어진 수열에서 순서는 유지한채로 숫자들을 선택하여 가장 긴 증가하는 수열을 찾아내는 문제입니다. 이 문제는 LIS(Longest Increasing Subsequence) 라고 합니다. 이 연습문제에서는 가장 긴 길이가 몇인지 구하기만 하면 됩니다.
풀이
동적계획법으로 쉽게 풀 수 있는 문제입니다. 최적부분구조, 중복되는 부분문제 이 2가지 조건을 만족하도록 부분문제를 어떻게 분할할 것인지를 생각해내는 것이 중요합니다.
그림과 같이 문제정의를 해야 합니다. 그러면 쉽게 관계식을 만들 수 있습니다. 이 관계식을 통해 최적부분구조 가 성립함을 알 수 있고, 부분문제의 종류는 N개 밖에 없으니 중복되는 부분문제가 발생합니다.
따라서 동적계획법을 사용하면 부분문제를 푸는데 O(N), 전체 부분문제의 개수는 N개 로 전체 시간복잡도가 O(N^2) 이 됩니다. 문제의 제약조건 N <= 1000 안에서 모두 해결할 수 있습니다.
전체 코드:
#include <stdio.h>
#define MAXN 1005
#define MAX(a,b) ((a<b) ? (b) : (a))
int N;
int a[MAXN], d[MAXN];
int main(void)
{
scanf("%d", &N);
for (int i = 0; i < N; i++)
scanf("%d", &a[i]);
for (int i = 0; i < N; i++)
d[i] = 1;
for (int i = 1; i < N; i++)
for (int j = 0; j < i; j++)
if (a[j] < a[i]) d[i] = MAX(d[i], d[j] + 1);
int ans = 0;
for (int i = 0; i < N; i++)
if (ans < d[i]) ans = d[i];
printf("%d\n", ans);
return 0;
}
이 문제는 최장 길이만 찾으면 되지만, 만약 어떤 부분 수열로 최장 길이가 되는지를 찾고 싶다면 dp[] 메모리값을 통해 어떤 수열로 구성되었는지를 알 수 있습니다. 이처럼 동적계획법 문제에서는 최적해뿐만 아니라 어떤 조합으로 최적해가 되는지도 구할 수 있습니다.
다른 연습문제 추천
- 1로 만들기: (https://www.acmicpc.net/problem/1463)
- 정수 삼각형: (https://www.acmicpc.net/problem/1932)
- 파일 합치기: (https://www.acmicpc.net/problem/11066)
- LCS: (https://www.acmicpc.net/problem/9251)
- 외판원 순회: (https://www.acmicpc.net/problem/2098)
동적계획법은 이 글에서 다루지 못한 테크닉도 너무 많아 연습문제가 수두룩하게 있습니다. 여러가지 문제를 직접 풀어보면서 접근 방식에 익숙해지면 많은 도움되실 것 같습니다.