넘파이(Numpy) 사용법 알아보기
in Machine Learning on Python, Tutorial, Numpy
넘파이 공식홈페이지 Quickstart tutorial에서 소개된 사용법을 따라하면서 정리한 글입니다. 실습해보면서 처음 시작하시는 분들도 이해할 수 있도록 설명을 추가하였으니 도움되시길 바랍니다.
이 글을 읽으신 후에 더 자세한 내용이 필요하시면 아래 링크를 확인하세요.
- Numpy
- 공식 홈페이지
- Documentation
- Quickstart Tutorial (이 글에서 소개된 내용)
- Scipy
목차
- 기본 개념 (The Basics)
- Shape 변경 (Shape Manipulation)
- 데이터 복사 (Copies and Views)
- 브로드캐스팅 (Broadcasting rules)
- 인덱싱 (Advanced Indexing and index tricks)
- 선형대수 (Linear Algebra)
Numpy
넘파이(Numpy)는 Python에서 벡터, 행렬 등 수치 연산을 수행하는 선형대수(Linear algebra) 라이브러리입니다. 선형대수 관련 수치 연산을 지원하고 내부적으로는 C로 구현되어 있어 연산이 빠른 속도로 수행됩니다. 또한 Scipy와 함께 사용하면 공학용 소프트웨어인 MATLAB에 버금가는 기능을 지원한다고 알려져 있습니다.
아래 Numpy 패키지를 추가하시길 바랍니다. 랜덤값을 생성해주는 .random도 사용하니 같이 추가해주세요
- 패키지가 없는 경우, 설치 명령어: pip install numpy
import numpy as np
import numpy.random as npr
1. 기초 개념 (The Basics)
Numpy에서 오브젝트는 동차(Homogeneous) 다차원 배열이라고 하는데 Homogeneous하다는 것은 수학적으로 긴 설명이 필요한데 단순히 다차원 배열로 표현한다고 이해하셔도 사용하는데 문제 없으니 넘어가겠습니다. Numpy에서는 모든 배열의 값이 기본적으로 같은 타입이어야 합니다. 그리고 Numpy에서는 각 차원(Dimension)을 축(axis)이라고 표현합니다.
3D Space의 포인트를 [1, 2, 1] 과 같은 배열로 표현가능 한데, 1개의 축을 가진다고 표현합니다. 또한 여기서 축은 3개의 요소(Element)를 가지고 있다고 하며 길이(Length)도 3입니다.
아래와 같은 데이터는 2개의 축을 가집니다. 1번째 축은 길이가 2이며, 2번째 축은 길이가 3입니다.
[[ 1, 0, 0],
[ 0, 1, 2]]
Numpy에서 배열은 ndarray 또는 array라고도 부릅니다. Numpy.array와 Python.array는 다릅니다. Numpy.ndarray의 다양한 속성값을 확인해보겠습니다.
예제 - An example
아래와 같이 (3, 5) 크기의 2D 배열을 생성할 수 있습니다. 지금은 코드를 몰라도 됩니다. 결과만 확인하세요.
a = np.arange(15).reshape(3, 5)
print(a)
# [[ 0 1 2 3 4]
# [ 5 6 7 8 9]
# [10 11 12 13 14]]
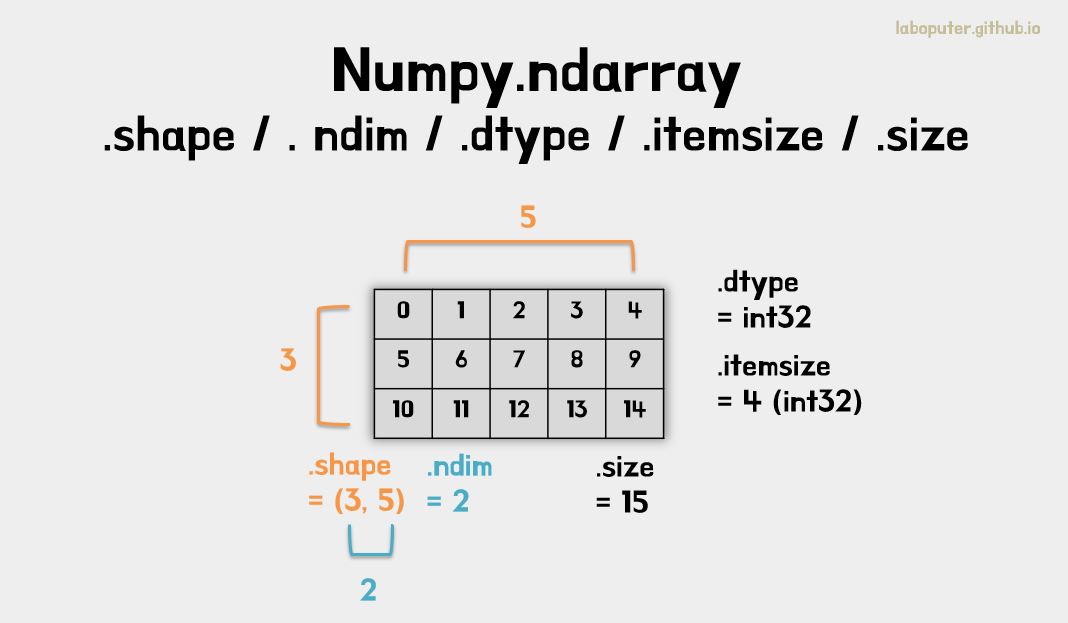
numpy.ndarray의 대표적인 속성값들은 다음과 같습니다.
- ndarray.shape : 배열의 각 축(axis)의 크기
- ndarray.ndim : 축의 개수(Dimension)
- ndarray.dtype : 각 요소(Element)의 타입
- ndarray.itemsize : 각 요소(Element)의 타입의 bytes 크기
- ndarray.size : 전체 요소(Element)의 개수
print(a.shape)
# (3, 5)
print(a.ndim)
# 2
print(a.dtype)
# int64
print(a.itemsize)
# 8
print(a.size)
# 15
print(type(a))
# <class 'numpy.ndarray'>
배열 생성하기 - Array Creation
np.array()를 이용하여 Python에서 사용하는 Tuple(튜플)이나 List(리스트)를 입력으로 numpy.ndarray를 만들 수 있습니다.
a = np.array([2,3,4])
print(a)
# [2 3 4]
print(a.dtype)
# int64
b = np.array([1.2, 3.5, 5.1])
print(b.dtype)
# float64
자주 발생하는 실수로 아래와 같이 여러개의 입력하는 것이 아니라 연속된 데이터를 입력으로 주어야 합니다.
a = np.array(1,2,3,4) # WRONG
print(a)
# ValueError: only 2 non-keyword arguments accepted
a = np.array([1,2,3,4]) # RIGHT
print(a)
2D 배열이나 3D 배열등도 마찬가지 방법으로 입력으로 주면 생성할 수 있습니다.
b = np.array([(1.5,2,3), (4,5,6)])
print(b)
# [[1.5 2. 3. ]
# [4. 5. 6. ]]
dtype = complex으로 복소수 값도 생성할 수 있습니다.
c = np.array( [ [1,2], [3,4] ], dtype = complex)
print(c)
# [[1.+0.j 2.+0.j]
# [3.+0.j 4.+0.j]]
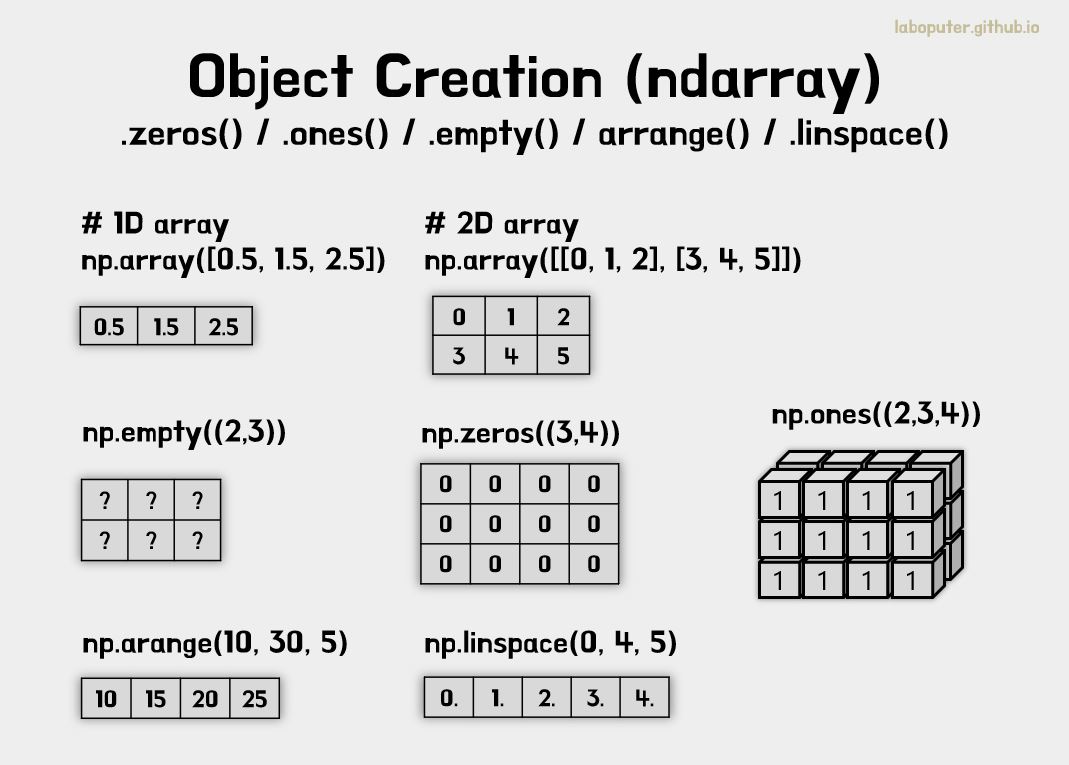
np.zeros(), np.ones(), np.empty()를 이용하여 다양한 차원의 데이터를 쉽게 생성할 수 있습니다.
np.zeros(shape): 0으로 구성된 N차원 배열 생성np.ones(shape): 1로 구성된 N차원 배열 생성np.empty(shape): 초기화되지 않은 N차원 배열 생성
#[3,4] 크기의 배열을 생성하여 0으로 채움
print(np.zeros((3,4)))
# [[0. 0. 0. 0.]
# [0. 0. 0. 0.]
# [0. 0. 0. 0.]]
# [2,3,4] 크기의 배열을 생성하여 1로 채움
print(np.ones((2,3,4), dtype=np.int16))
# [[[1 1 1 1]
# [1 1 1 1]
# [1 1 1 1]]
# [[1 1 1 1]
# [1 1 1 1]
# [1 1 1 1]]]
# 초기화 되지 않은 [2,3] 크기의 배열을 생성
print(np.empty((2,3)))
# [[1.39069238e-309 1.39069238e-309 1.39069238e-309]
# [1.39069238e-309 1.39069238e-309 1.39069238e-309]]
np.arange() 와 np.linspace()를 이용하여 연속적인 데이터도 쉽게 생성할 수 있습니다.
np.arange(): N 만큼 차이나는 숫자 생성np.linspace(): N 등분한 숫자 생성
# 10이상 30미만 까지 5씩 차이나게 생성
print(np.arange(10, 30, 5))
# [10 15 20 25]
# 0이상 2미만 까지 0.3씩 차이나게 생성
print(np.arange(0, 2, 0.3))
# [0. 0.3 0.6 0.9 1.2 1.5 1.8]
# 0~99까지 100등분
x = np.linspace(0, 99, 100)
print(x)
# [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17.
# 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35.
# 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53.
# 54. 55. 56. 57. 58. 59. 60. 61. 62. 63. 64. 65. 66. 67. 68. 69. 70. 71.
# 72. 73. 74. 75. 76. 77. 78. 79. 80. 81. 82. 83. 84. 85. 86. 87. 88. 89.
# 90. 91. 92. 93. 94. 95. 96. 97. 98. 99.]
배열 출력하기 - Printing Arrays
1D와 2D 배열은 설명하지 않아도 어떻게 출력되는지 확인하실 수 있으나, 3D 배열은 2차원이 N개 출력되는 형식으로 나타납니다.
a = np.arange(6)
print(a)
# [0 1 2 3 4 5]
b = np.arange(12).reshape(4,3)
print(b)
# [[ 0 1 2]
# [ 3 4 5]
# [ 6 7 8]
# [ 9 10 11]]
c = np.arange(24).reshape(2,3,4)
print(c)
# [[[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
#
# [[12 13 14 15]
# [16 17 18 19]
# [20 21 22 23]]]
np.ndarray.reshape()을 통해 데이터는 그대로 유지한 채 차원을 쉽게 변경해줍니다.
# [10000] 배열을 [100, 100] 배열로 변경
print(np.arange(10000).reshape(100,100))
# [ 0 1 2 ... 9997 9998 9999]
# [[ 0 1 2 ... 97 98 99]
# [ 100 101 102 ... 197 198 199]
# [ 200 201 202 ... 297 298 299]
# ...
# [9700 9701 9702 ... 9797 9798 9799]
# [9800 9801 9802 ... 9897 9898 9899]
# [9900 9901 9902 ... 9997 9998 9999]]
기본 연산 - Basic Operations
numpy에서 수치연산은 기본적으로 element wise 연산입니다. 숫자가 각각의 요소에 연산이 적용됩니다.
a = np.array( [20,30,40,50] )
b = np.arange( 4 )
print(b)
# [0 1 2 3]
# a에서 b에 각각의 원소를 -연산
c = a-b
print(c)
# [20 29 38 47]
# b 각각의 원소에 제곱 연산
print(b**2)
# [0 1 4 9]
# a 각각의 원소에 *10 연산
print(10*np.sin(a))
# [ 9.12945251 -9.88031624 7.4511316 -2.62374854]
# a 각각의 원소가 35보다 작은지 Boolean 결과
print(a<35)
# [ True True False False]
2차원 배열을 행렬이라고 생각했을 때 행렬의 여러가지 곱셈이 있습니다.
*: 각각의 원소끼리 곱셈 (Elementwise product, Hadamard product)@: 행렬 곱셈 (Matrix product).dot(): 행렬 내적 (dot product)
A = np.array( [[1,1],
[0,1]] )
B = np.array( [[2,0],
[3,4]] )
print(A * B)
# [[2 0]
# [0 4]]
print(A @ B)
# [[5 4]
# [3 4]]
print(A.dot(B))
# [[5 4]
# [3 4]]
수치연산 진행할 때 각각의 .dtype이 다르면 타입이 큰쪽(int < float < complex)으로 자동으로 변경됩니다.
a = np.ones(3, dtype=np.int32)
b = np.linspace(0, np.pi,3)
print(b.dtype.name)
# float64
# a(int), b(float) 연산 시 float로 upcasting
c = a+b
print(c)
# [1. 2.57079633 4.14159265]
print(c.dtype.name)
# float64
# 마찬가지로 복소수 연산 시 complex(복소수)로 upcasting
d = np.exp(c*1j)
print(d)
# [ 0.54030231+0.84147098j -0.84147098+0.54030231j -0.54030231-0.84147098j]
print(d.dtype.name)
# complex128
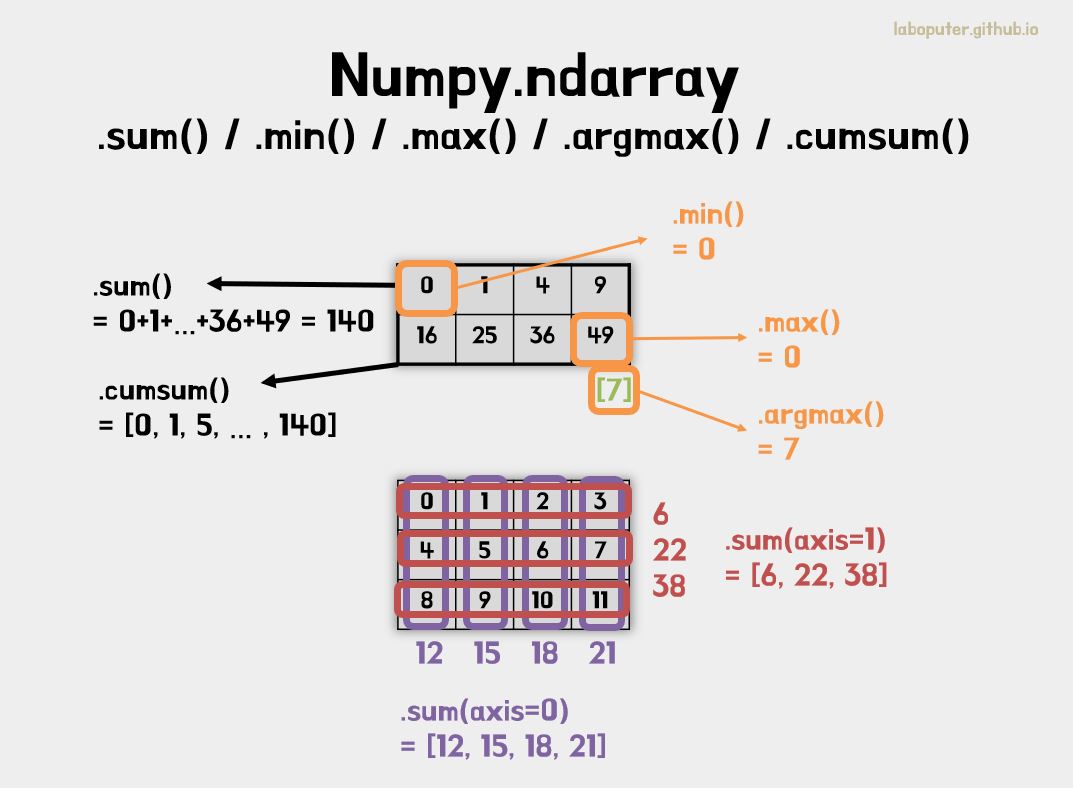
.sum(), .min(), .max(), .argmax(), .cumsum()와 같은 연산을 진행할 수 있습니다.
.sum(): 모든 요소의 합.min(): 모든 요소 중 최소값.max(): 모든 요소 중 최대값.argmax(): 모든 요소 중 최대값의 인덱스.cumsum(): 모든 요소의 누적합
a = np.arange(8).reshape(2, 4)**2
print(a)
# [[ 0 1 4 9]
# [16 25 36 49]]
# 모든 요소의 합
print(a.sum())
# 140
# 모든 요소 중 최소값
print(a.min())
# 0
# 모든 요소 중 최대값
print(a.max())
# 49
# 모든 요소 중 최대값의 인덱스
print(a.argmax())
# 7
# 모든 요소의 누적합
print(a.cumsum())
# [ 0 1 5 14 30 55 91 140]
.sum(), .min(), .max(), .cumsum()과 같은 연산에 axis 값을 입력하면 축을 기준으로도 연산할 수 있습니다. axis=0은 shape에서 첫번째부터 순서대로 해당됩니다.
b = np.arange(12).reshape(3,4)
print(b)
# [[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
print(b.sum(axis=0))
# [12 15 18 21]
print(b.sum(axis=1))
# [ 6 22 38]
범용 함수 - Universal Functions
수학적인 연산이 너무 많아 .exp(), .sqrt()만 사용해봅니다. 필요한 수치연산은 available-ufuncs을 확인하세요.
B = np.arange(3)
print(B)
# [0 1 2]
# y = e^x
print(np.exp(B))
# [1. 2.71828183 7.3890561 ]
# y = sqrt(x)
print(np.sqrt(B))
# [0. 1. 1.41421356]
인덱싱, 슬라이싱, 반복 - Indexing, Slicing and Iterating
Numpy에서 인덱싱과 슬라이싱에 대한 개념은 Python과 기본적으로 동일합니다. 설명이 필요하신 분은 5. 인덱싱 에서 다시 다룹니다.
a = np.arange(10)**3
print(a)
# [ 0 1 8 27 64 125 216 343 512 729]
print(a[2])
# 8
# 2~4번 인덱스
print(a[2:5])
# [ 8 27 64]
# 0~5번에서 2Step 인덱스
a[:6:2] = 1000
print(a)
# [1000 1 1000 27 1000 125 216 343 512 729]
# reverse
a[ : :-1]
for i in a:
print(i**(1/3.))
# 9.999999999999998
# 1.0
# 9.999999999999998
# 3.0
# 9.999999999999998
# 4.999999999999999
# 5.999999999999999
# 6.999999999999999
# 7.999999999999999
# 8.999999999999998
np.fromfunction()을 통해 인덱스 번호를 가지고 함수를 정의해 생성할 수도 있습니다.
def f(x,y):
return 10*x+y
b = np.fromfunction(f, (5,4), dtype=int)
print(b)
# [[ 0 1 2 3]
# [10 11 12 13]
# [20 21 22 23]
# [30 31 32 33]
# [40 41 42 43]]
print(b[2,3])
# 23
print(b[0:5, 1])
# [ 1 11 21 31 41]
print(b[ : ,1])
# [ 1 11 21 31 41]
print(b[1:3, : ])
# [[10 11 12 13]
# [20 21 22 23]]
print(b[-1])
# [40 41 42 43]
...은 차원이 너무 많을 때 실수를 줄여줄 수 있습니다. 만약 x가 5차원이라고 할 때 아래 처럼 표현할 수 있습니다.
- x[1, 2, …] 는 x[1, 2, :, :, :] 와 같습니다.
- x[…, 3] 는 x[:, :, :, :, 3] 와 같습니다.
- x[4, …, 5, :] 는 x[4, :, :, 5, :] 와 같습니다.
# a 3D array (two stacked 2D arrays)
c = np.array( [[[ 0, 1, 2],
[ 10, 12, 13]],
[[100,101,102],
[110,112,113]]])
print(c.shape)
# (2, 2, 3)
print(c[1,...]) # same as c[1,:,:] or c[1]
# [[100 101 102]
# [110 112 113]]
print(c[...,2]) # same as c[:,:,2]
# [[ 2 13]
# [102 113]]
다차원의 배열을 for문을 적용하면 axis=0 기준으로 적용됩니다. 만약 다차원 배열의 모든 원소를 for문 적용하고 싶은 경우 .reshape()을 해도 되지만, .flat을 이용할 수 있습니다.
for row in b:
print(row)
# [0 1 2 3]
# [10 11 12 13]
# [20 21 22 23]
# [30 31 32 33]
# [40 41 42 43]
for element in b.flat:
print(element)
# 0
# 1
# 2
# 3
# 10
# 11
# 12
# 13
# 20
# 21
# 22
# 23
# 30
# 31
# 32
# 33
# 40
# 41
# 42
# 43
2. Shape 변경 (Shape Manipulation)
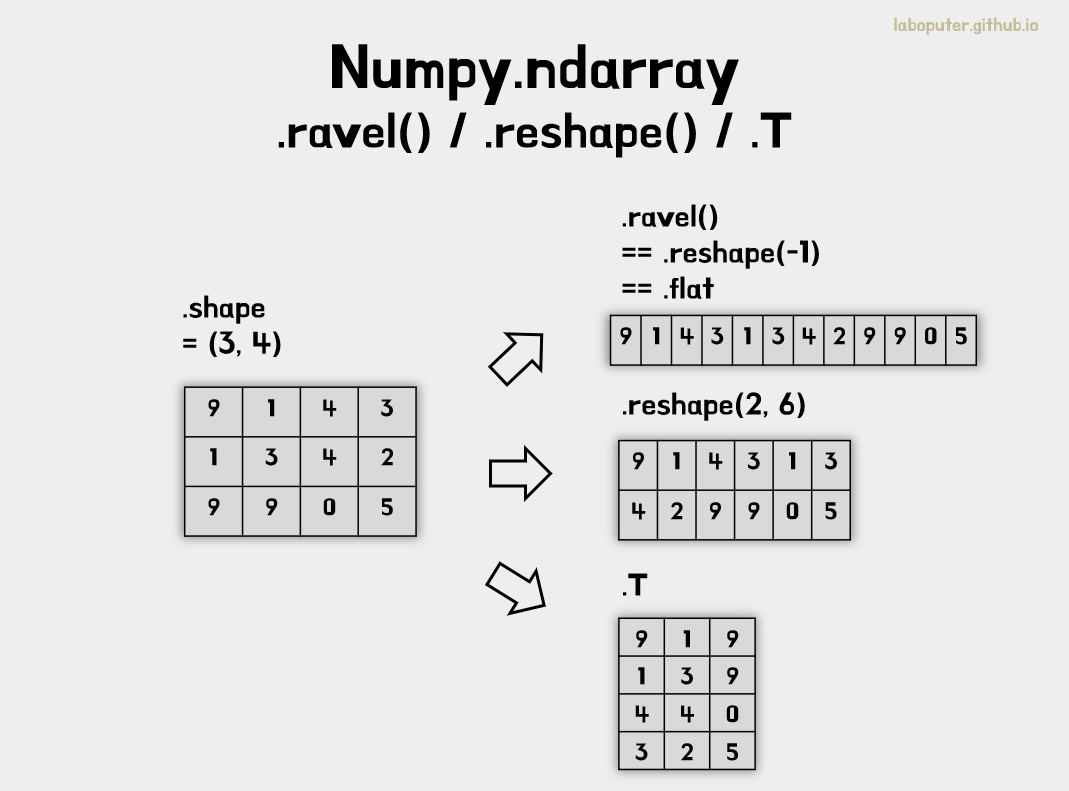
np.ndarray의 shape를 다양한 방법으로 변경할 수 있습니다. .ravel()은 1차원으로, .reshape()는 지정한 차원으로, .T는 전치(Transpose) 변환을 할 수 있습니다. 하지만 데이터 원본은 변경시키지 않고 복사하여 연산한 결과가 return 됩니다.
a = np.floor(10*npr.random((3,4)))
print(a)
# [[8. 0. 0. 6.]
# [1. 4. 3. 0.]
# [0. 3. 1. 9.]]
print(a.shape)
# (3, 4)
# 모든 원소를 1차원으로 변경
print(a.ravel())
# [8. 0. 0. 6. 1. 4. 3. 0. 0. 3. 1. 9.]
# [3,4] => [2,6]로 변경
print(a.reshape(2,6))
# [[8. 0. 0. 6. 1. 4.]
# [3. 0. 0. 3. 1. 9.]]
# [3,4]의 전치(transpose)변환으로 [4,3]
print(a.T)
# [[8. 1. 0.]
# [0. 4. 3.]
# [0. 3. 1.]
# [6. 0. 9.]]
print(a.T.shape)
# (4, 3)
print(a.shape)
# (3, 4)
.resize()는 위의 .reshape()와 동일한 기능이지만 원본 데이터 자체를 변경시킵니다. .reshape()를 할 때 차원값에 -1를 입력하면 -1 부분은 자동으로 차원을 채워줍니다. 당연히 여러 차원에서 -1는 하나만 사용할 수 있고 나머지가 지정된 결과를 바탕으로 자동으로 계산해줍니다
print(a)
# [[8. 0. 0. 6.]
# [1. 4. 3. 0.]
# [0. 3. 1. 9.]]
a.resize((2,6))
print(a)
# [[8. 0. 0. 6. 1. 4.]
# [3. 0. 0. 3. 1. 9.]]
print(a.reshape(3,-1))
# [[8. 0. 0. 6.]
# [1. 4. 3. 0.]
# [0. 3. 1. 9.]]
데이터 쌓기 - Stacking together different arrays
np.vstack() 와 np.hstack()를 통해 데이터를 합칠 수 있습니다.
np.vstack(): axis=0 기준으로 쌓음np.hstack(): axis=1 기준으로 쌓음
a = np.floor(10*npr.random((2,2)))
print(a)
# [[1. 4.]
# [2. 4.]]
b = np.floor(10*npr.random((2,2)))
print(b)
# [[3. 7.]
# [3. 7.]]
# [2,2] => [4,2]
print(np.vstack((a,b)))
# [[1. 4.]
# [2. 4.]
# [3. 7.]
# [3. 7.]]
# [2,2] => [2,4]
print(np.hstack((a,b)))
# [[1. 4. 3. 7.]
# [2. 4. 3. 7.]]
데이터 쪼개기 - Splitting one array into several smaller ones
np.hsplit()을 통해 숫자1개가 들어갈 경우 X개로 등분, 리스트로 넣을 경우 axis=1 기준 인덱스로 데이터를 분할할 수 있습니다.
a = np.floor(10*npr.random((2,12)))
print(a)
# [[4. 4. 1. 7. 7. 8. 8. 8. 4. 3. 5. 3.]
# [9. 8. 7. 5. 6. 8. 9. 6. 9. 5. 4. 7.]]
# [2,12] => [2,4] 데이터 3개로 등분
print(np.hsplit(a, 3))
# [array([[4., 4., 1., 7.],
# [9., 8., 7., 5.]]), array([[7., 8., 8., 8.],
# [6., 8., 9., 6.]]), array([[4., 3., 5., 3.],
# [9., 5., 4., 7.]])]
# [2,12] => [:, :3], [:, 3:4], [:, 4:]로 분할
print(np.hsplit(a, (3,4)))
# [array([[4., 4., 1.],
# [9., 8., 7.]]), array([[7.],
# [5.]]), array([[7., 8., 8., 8., 4., 3., 5., 3.],
# [6., 8., 9., 6., 9., 5., 4., 7.]])]
3. 데이터 복사 (Copies and Views)
복사되지 않는 경우 - No Copy at All
아래와 같이 np.array를 변수에 넣는다고 해서 복사가 되지 않습니다. 레퍼런스를 참조할 뿐입니다. id()를 통해 주소값을 반환해서 확인할 수 있습니다.
a = np.array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
# 두 개가 사실상 같습니다. (복사가 아님)
b = a
print(b is a)
# True
print(id(a))
# 140389588429040
print(id(b))
# 140389588429040
얕은복사 - View or Shallow Copy
view()를 통해 Shallow Copy를 할 수 있습니다. Shallow Copy, Deep Copy의 개념을 이해하고 있다면 이것으로 이해하실 수 있을 것입니다. Numpy 관점에서 쉽게 설명드리면 view()는 실제로 데이터가 복사된다기 보다는 데이터 각각의 참조값이 복사됩니다. c와 a의 참조값은 다르지만 각각의 데이터 참조값이 복사됐다는 의미입니다. 따라서 a와 c는 다르지만 c[0, 4]는 a[0, 4]는 같은 참조값을 보고 있어 a가 변경되는 것을 확인할 수 있습니다. 마찬가지로 s에 a를 슬라이싱하여 데이터를 가져가도 s를 변경하면 a가 변경됩니다.
c = a.view()
# c와 a의 참조값은 다름
print(c is a)
# False
c = c.reshape((2, 6))
print(a.shape)
# (3, 4)
# c의 데이터와 a의 데이터의 참조값은 같음
c[0, 4] = 1234
print(a)
# [[ 0 1 2 3]
# [1234 5 6 7]
# [ 8 9 10 11]]
# a를 슬라이싱해도 데이터의 참조값은 같음
s = a[ : , 1:3]
s[:] = 10
print(a)
# [[ 0 10 10 3]
# [1234 10 10 7]
# [ 8 10 10 11]]
깊은복사 - Deep copy
.copy()를 이용하면 Deep Copy를 할 수 있습니다. 즉 a와 d의 참조값 뿐만 아니라 a의 각각의 데이터 전부가 새로운 객체로 생성됩니다.
d = a.copy()
# a와 d의 참조값은 다름
print(d is a)
# False
# a와 d의 데이터의 참조값도 다름
d[0,0] = 9999
print(a)
# [[ 0 10 10 3]
# [1234 10 10 7]
# [ 8 10 10 11]]
Python의 del 키워드를 이용하면 메모리를 반환할 수 있습니다.
a = np.arange(int(1e8))
b = a[:100].copy()
del a
print(a)
# ---------------------------------------------------------------------------
# NameError Traceback (most recent call last)
# <ipython-input-32-2dcfdd85bd07> in <module>()
# 2 b = a[:100].copy()
# 3 del a
# ----> 4 print(a)
# NameError: name 'a' is not defined
4. 브로드캐스팅 (Broadcasting rules)
Numpy에서 Broadcasting(브로드캐스팅)은 반드시 이해하고 있어야 하는 개념이어서 그림과 함께 설명하겠습니다. 브로드 캐스팅은 단순하게 편리성을 위해 Shape가 다른 np.narray 끼리 연산을 지원해주기 위함입니다. 데이터 계산 시 자주 등장하는 상황인데, 이것이 없다면 Shape를 맞춰야하는 번거로움이 생기게 되는데 이 개념을 이해하면 잘 활용하실 수 있습니다. 웬만하면 Shape를 같게 맞춘 후에 연산하는 것이 바람직하지만 이 글에서도 알게 모르게 사용하고 있었습니다.
np.array([1,2,3,4,5]) * 2
# 결과
# [2,4,6,8,10]
위와 같은 연산을 많이 보셨을 겁니다. 일반적인 Python List였으면 값이 10개인 배열이 생성되지만, 이렇게 계산되는 이유는 Numpy의 브로드 캐스팅의 결과로 내부적으로 아래 변환되어 계산됩니다.
np.array([1,2,3,4,5]) * 2
# Broadcasting
np.array([1,2,3,4,5]) * np.array([2,2,2,2,2])
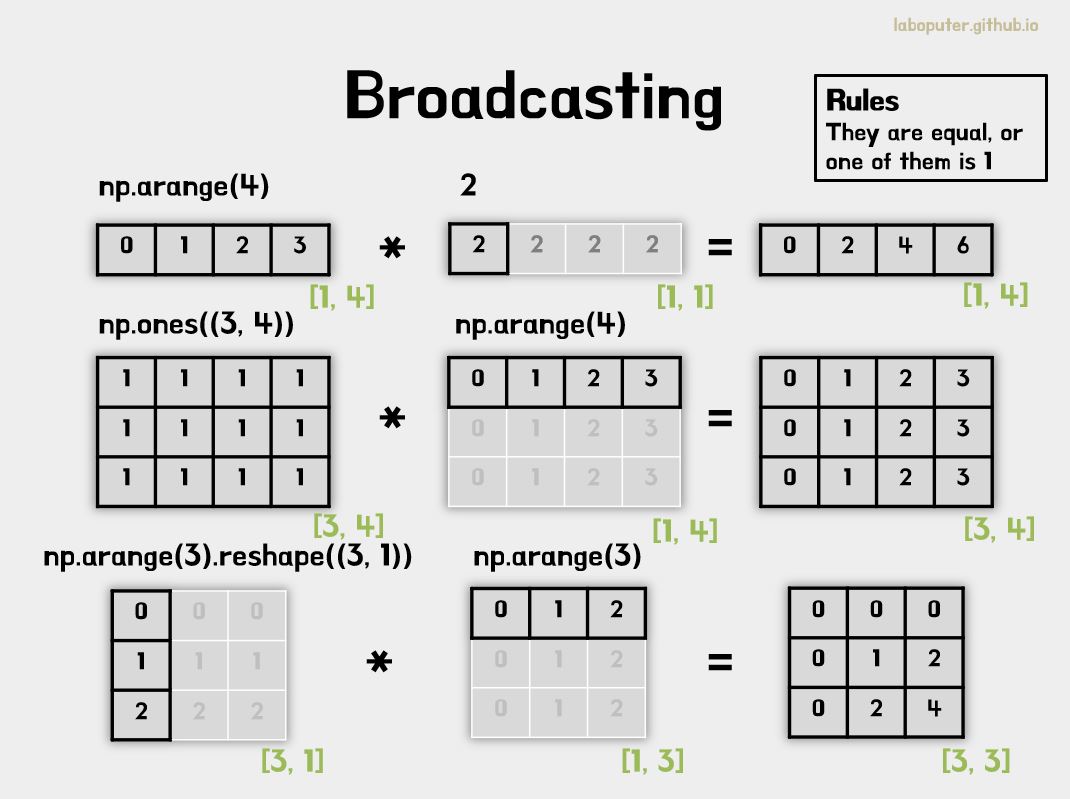
우선 차원(ndim)이 같고 각 축(axis)의 값이 같거나 1이야 연산이 가능합니다. 만약 각 축의 값이 다르면 브로드캐스팅되어 값이 복사됩니다. 아래 코드 및 그림으로 확인하세요.
자세한 내용은 Broadcasting을 확인하세요.
print(np.arange(4) * 2)
# [0 2 4 6]
print(np.ones((3,4)) * np.arange(4))
# [[0. 1. 2. 3.]
# [0. 1. 2. 3.]
# [0. 1. 2. 3.]]
print(np.arange(3).reshape((3,1)) * np.arange(3))
# [[0 0 0]
# [0 1 2]
# [0 2 4]]
5. 인덱싱 (Advanced Indexing and index tricks)
인덱스 배열로 인덱싱하기 - Indexing with Arrays of Indices
인덱스를 가진 배열로 인덱싱을 할 수 있습니다.
a = np.arange(12)**2
print(a)
# [ 0 1 4 9 16 25 36 49 64 81 100 121]
i = np.array([1, 1, 3, 8, 5])
print(a[i])
# [ 1 1 9 64 25]
j = np.array([[3, 4], [9, 7]])
print(a[j])
# [[ 9 16]
# [81 49]]
그림을 이해하셨으면 아래 인덱싱 코드들은 설명이 되실겁니다.
palette = np.array([[0, 0, 0], # black
[255, 0, 0], # red
[0, 255, 0], # green
[0, 0, 255], # blue
[255, 255, 255]]) # white
image = np.array([[0, 1, 2, 0],
[0, 3, 4, 0]])
palette[image]
# array([[[ 0, 0, 0],
# [255, 0, 0],
# [ 0, 255, 0],
# [ 0, 0, 0]],
# [[ 0, 0, 0],
# [ 0, 0, 255],
# [255, 255, 255],
# [ 0, 0, 0]]])
a = np.arange(5)
print(a)
# [0 1 2 3 4]
a[[1,3,4]] = 0
print(a)
# [0 0 2 0 0]
a = np.arange(5)
print(a)
# [0 1 2 3 4]
a[[0,0,2]] += 1
print(a)
# [1 1 3 3 4]
Bool로 인덱싱하기 - Indexing with Boolean Arrays
Bool 타입을 가진 값들로도 인덱싱이 가능합니다.
a = np.arange(12).reshape(3,4)
b = a > 4
print(b)
# [[False False False False]
# [False True True True]
# [ True True True True]]
print(a[b])
# [ 5 6 7 8 9 10 11]
a[b] = 0
print(a)
# [[0 1 2 3]
# [4 0 0 0]
# [0 0 0 0]]
Mandelbrot Set이라고 하는 프랙탈 모형이 있습니다. 이 값은 복소수의 집합으로 정의된 것인데 이런 것들도 구현이 가능함을 볼 수 있습니다.
import numpy as np
import matplotlib.pyplot as plt
def mandelbrot( h,w, maxit=20 ):
"""Returns an image of the Mandelbrot fractal of size (h,w)."""
y,x = np.ogrid[ -1.4:1.4:h*1j, -2:0.8:w*1j ]
c = x+y*1j
z = c
divtime = maxit + np.zeros(z.shape, dtype=int)
for i in range(maxit):
z = z**2 + c
diverge = z*np.conj(z) > 2**2 # who is diverging
div_now = diverge & (divtime==maxit) # who is diverging now
divtime[div_now] = i # note when
z[diverge] = 2 # avoid diverging too much
return divtime
plt.imshow(mandelbrot(400,400))

The ix_() function
.ix_()을 통해 서로 다른 Shape를 가진 배열들을 묶어서 처리할 수 있습니다.
a = np.array([2,3,4,5])
b = np.array([8,5,4])
c = np.array([5,4,6,8,3])
ax,bx,cx = np.ix_(a,b,c)
print(ax)
# [[[2]]
# [[3]]
# [[4]]
# [[5]]]
print(bx)
# [[[8]
# [5]
# [4]]]
print(cx)
# [[[5 4 6 8 3]]]
print(ax.shape, bx.shape, cx.shape)
# (4, 1, 1) (1, 3, 1) (1, 1, 5)
result = ax+bx*cx
print(result)
# [[[42 34 50 66 26]
# [27 22 32 42 17]
# [22 18 26 34 14]]
# [[43 35 51 67 27]
# [28 23 33 43 18]
# [23 19 27 35 15]]
# [[44 36 52 68 28]
# [29 24 34 44 19]
# [24 20 28 36 16]]
# [[45 37 53 69 29]
# [30 25 35 45 20]
# [25 21 29 37 17]]]
print(result[3,2,4])
# 17
print(a[3]+b[2]*c[4])
# 17
6. 선형대수 (Linear Algebra)
실제로 선형대수 연산은 아래와 같이 진행할 수 있는데 선형대수는 글의 주제에 벗어나므로 설명은 생략하겠습니다.
a = np.array([[1.0, 2.0], [3.0, 4.0]])
print(a)
# [[1. 2.]
# [3. 4.]]
a.transpose()
np.linalg.inv(a)
# unit 2x2 matrix; "eye" represents "I"
u = np.eye(2)
u
# matrix product
j = np.array([[0.0, -1.0], [1.0, 0.0]])
j @ j
# trace
np.trace(u)
y = np.array([[5.], [7.]])
np.linalg.solve(a, y)
np.linalg.eig(j)
# (array([0.+1.j, 0.-1.j]),
# array([[0.70710678+0.j , 0.70710678-0.j ],
# [0. -0.70710678j, 0. +0.70710678j]]))
이 포스팅에서 사용한 코드는 이곳에 공개되어 있으며 다운로드 받으실 수 있습니다.