[Dataset] 신용카드 사기 거래 감지하기
in Machine Learning on Kaggle, Autoencoder, Anomaly-detection, Tutorial
신용카드 사기 거래 감지(Credit card fraud detection)를 통해 데이터 분석 및 모델링에 입문하는 것을 목표로 합니다. 실제 카드 거래내역으로 부터 사기 거래 여부를 판별하기 위한 머신러닝과 딥러닝 모델로 학습하는 것과 모델에 대한 평가지표를 정리하였습니다.
개요
Credit Card Fraud Detection
캐글에서 제공하는 (Dataset) Credit Card Fraud Dectection에서 데이터를 다운로드 받을 수 있습니다. 이 데이터는 2013년 9월 유럽의 신용카드 사용자들의 실제 거래기록으로 총 284,807 건의 거래내역이 제공됩니다. 이 중 492건이 사기 거래(Fraud Transaction)이고 사기 거래가 정상 거래에 비해 매우 적은 0.172%로 ‘Highly unbalanced’한 특징을 가진 데이터셋입니다.
Highly unbalanced datasets
이러한 형태의 데이터셋은 아무런 예측을 하지 않고 모두 정상이라고 판단해도 정확도(Accuracy)가 99.83%로 아주 높습니다. 이렇게 정확도(Accuracy)라는 수치로는 좋은 모델인지 쉽게 평가할 수 없기 때문에 이러한 문제에서는 별도의 평가지표로 모델의 정확성을 판단하는 것이 좋습니다. 또한 일반적으로 이런 문제는 실제 사기 거래인 데이터를 확보하기도 어려운 경우가 많습니다.
따라서 이 포스팅은 신용카드 사기 거래 감지하기(Credit Card Fraud Detection) 문제를 통해 Highly unbalnced한 데이터셋을 다루기 위한 모델 평가 지표와 레이블 을 알 수 없는 데이터 (사기 거래인지 모르는)를 어떻게 접근했는지를 정리한 내용입니다.
분류 문제의 평가지표 ‘F1-score’
분류 문제, 특히 정상/비정상과 같이 2가지 중 하나로 분류해야 하는 Binary Classification 문제에서는 아래 그림과 같이 4가지 경우의 수로 나타납니다.
각 경우의 수를 어떻게 계산하느냐에 따라 여러 가지 의미를 가지는 지표들이 있습니다. Accuracy(정확도), Precision(정밀도), Recall(재현율), F1-score인데 각각 무엇을 의미할까요?
- Accuracy(정확도): 모든 예측(True 또는 False)이 실제로 맞은 비율
- Precision(정밀도): ‘True’ 라고 예측한 것 중 실제로 ‘True’ 인 비율
- Recall(재현율): 모든 ‘True’인 것 중 ‘True’로 예측한 것의 비율
- F1-score: 정밀도, 재현율의 조화평균
예를 들어 1개의 거래만 ‘사기’라고 예측해서 실제로 맞히면 Precision은 1(100%) 입니다. 한번의 시도가 맞았으니까요. 반면에 전체 거래가 ‘사기’라고 예측하면 Recall은 무조건 1(100%) 입니다. 모든 ‘사기’ 거래를 예측해냈으니까요. 이상한 지표 같지만 사실 이 각각의 지표가 갖는 바가 중요합니다. Precision을 높이면 Recall이 낮아지고, 반대로 Recall을 높이면 Precision이 낮아질 수 밖에 없는 관계거든요.
우리가 기상청이라고 가정해봅시다. ‘오보청’ 이라는 오명을 벗어나기 위해 강수확률이 90% 이상으로 매우 높을 때만 우천 방송을 한다고 기준을 세웠습니다. 그럼 비 온다고 방송하면 실제 비가 올 확률은 높지만(Precision이 높은) 강수확률이 60~80% 일 때도 비가 온다면 비온 것을 예보하지 못하는 경우가 많은(Recall이 낮은) 불상사가 생깁니다. 그렇다고 강수확률이 60% 이상일 때 우천 방송을 한다면, 비가 오지 않을 경우가 많아(Precision이 낮은) 욕을 먹게 될 것입니다. 사람들은 비 온다고 방송하면 실제로 비가 오고, 비가 오지 않는다고 방송하면 실제로 오지 않는 그런 기상청을 원하기 때문입니다.
그래서 우리는 Precision, Recall 중 어느 하나에 치우친 지표가 아니라 Precision과 Recall의 조화평균인 F1-score를 이 포스팅에서 가장 중요한 평가지표로 다룰 것입니다.
자세한 내용은 F1 Score (Wiki)를 확인하세요.
Step 1. EDA
가장 먼저 할일은 EDA (Exploratory Data Analysis)로 주어진 데이터가 어떤 형태인지 각자 자유롭게 파악하는 것입니다.
(Dataset) Credit Card Fraud Dectection에서 데이터를 다운로드 받은 후에 다음과 같이 데이터를 불러 옵니다.
import pandas as pd
data = pd.read_csv('creditcard.csv')
총 284,807 건의 거래데이터가 있으며 각 Column 정보는 아래와 같습니다.
- V1 ~ V28 : 개인정보로 공개되지 않은 값
- Time : 시간
- Amount : 거래금액
- Class : 사기 여부 (1: 사기, 0: 정상)
총 31개 Column이 있으며 이 중 시간과 거래금액을 뺀 V1 ~ V28 데이터로 부터 사기 여부(Class)를 예측하는 것을 목표로 합니다.
data.shape
# (284807, 31)
data.head()
| Time | V1 | V2 | ... | V21 | V22 | Amount | Class | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | -1.359807 | -0.072781 | ... | 0.133558 | -0.021053 | 149.62 | 0 |
| 1 | 0.0 | 1.191857 | 0.266151 | ... | -0.008983 | 0.014724 | 2.69 | 0 |
| 2 | 1.0 | -1.358354 | -1.340163 | ... | -0.055353 | -0.059752 | 378.66 | 0 |
| 3 | 1.0 | -0.966272 | -0.185226 | ... | 0.062723 | 0.061458 | 123.50 | 0 |
| 4 | 2.0 | -1.158233 | 0.877737 | ... | 0.219422 | 0.215153 | 69.99 | 0 |
5 rows × 31 columns
총 284,807 건의 거래데이터 중 492건만이 사기 거래 데이터임을 알 수 있습니다.
tmp = data['Class'].value_counts().to_frame().reset_index()
tmp['Percent(%)'] = tmp["Class"].apply(lambda x : round(100*float(x) / len(data), 2))
tmp = tmp.rename(columns = {"index" : "Target", "Class" : "Count"})
tmp
| Target | Count | Percent(%) | |
|---|---|---|---|
| 0 | 0 | 284315 | 99.83 |
| 1 | 1 | 492 | 0.17 |
Step 2. Data Engneering
다음 해야할 것은 데이터 엔지니어링(Data Engneering)으로 데이터를 학습하기 좋게 데이터를 다듬기도 하고, 새로운 특징(Feature)을 찾아 내기도 합니다. 이 데이터셋은 결측데이터도 없고, 이미 어느정도 다듬어진 상태이기 때문에 특별히 건드릴 것은 없습니다.
다만 사용하고자 하는 Feature(‘V1’ ~ ‘V28’)와 사기 여부(‘Class’) 데이터만 가져와서 Feature(x)와 Label(y)을 분리하겠습니다.
x_data = data.loc[:, 'V1' : 'V28']
y_data = data.loc[:, 'Class']
print(x_data.shape)
print(y_data.shape)
# (284807, 28)
# (284807,)
데이터를 랜덤하게 섞은 후에 Train, Test 데이터를 각각 7:3 으로 나누었습니다.
shuffle_index = np.random.permutation(len(data))
x_data = x_data.values[shuffle_index]
y_data = y_data.values[shuffle_index]
n_train = int(len(x_data) * 0.7)
x_train = x_data[:n_train]
y_train = y_data[:n_train]
x_test = x_data[n_train:]
y_test = y_data[n_train:]
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
# (199364, 28)
# (199364,)
# (85443, 28)
# (85443,)
Train, Test 데이터를 각각 사기/정상 으로 분류하여 보면 다음과 같습니다.
pd.DataFrame([[sum(y_train == 0), sum(y_test == 0)], [sum(y_train == 1), sum(y_test == 1)]],
columns=['train', 'test'], index=['0 (non-fraud)', '1 (fraud)'])
| train | test | |
|---|---|---|
| 0 (non-fraud) | 199022 | 85293 |
| 1 (fraud) | 342 | 150 |
Step 3. Modeling
이제 실제로 학습모델을 만들어 데이터를 학습한 후 신용카드 사기 거래를 감지하는 모델을 생성해보겠습니다. 첫번째로 접근할 방식은 머신러닝 기법 중 RandomForest라는 방법으로 학습해보겠습니다.
Modeling1 - RandomForest
sklearn 패키지를 이용하여 머신러닝 기법인 RandonForest를 이용하여 학습시켰습니다.
from sklearn.ensemble import RandomForestClassifier
# modeling
model_rf = RandomForestClassifier(n_estimators = 15)
# train
model_rf.fit(x_train, y_train)
# predict
y_pred = model_rf.predict(x_test)
y_real = y_test
train 데이터로 학습하고 test 데이터로 예측하여 평가지표를 계산하면 다음과 같습니다.
accuracy = round(sum(y_pred == y_real) / len(y_pred), 4)
precision = round(sum([p == 1 & r == 1 for p, r in zip(y_pred, y_real)]) / sum(y_pred == 1), 4)
recall = round(sum([p == 1 & r == 1 for p, r in zip(y_pred, y_real)]) / sum(y_real == 1), 4)
f1 = round(2 / ((1/precision) + (1/recall)), 4)
print('Accuracy : ', accuracy)
print('Precision : ', precision)
print('Recall : ', recall)
print('f1-score : ', f1)
# Accuracy : 0.9995
# Precision : 0.931
# Recall : 0.7714
# f1-score : 0.8437
precision, recall, f1-score도 sklearn 의 classification_report를 이용하면 쉽게 계산할 수 있습니다.
from sklearn.metrics import classification_report
print(classification_report(y_real, y_pred))
# precision recall f1-score support
# 0 1.00 1.00 1.00 85303
# 1 0.93 0.77 0.84 140
# accuracy 1.00 85443
# macro avg 0.97 0.89 0.92 85443
# weighted avg 1.00 1.00 1.00 85443
우리는 사기 거래라고 예측하면 92% 확률로 실제 사기 거래이고, 전체 사기 거래 중 무려 79%를 감지해내는 모델을 만들어 냈습니다. F1-score도 84% 로 꽤 괜찮은 것 같습니다.
Modeling 2 - Logistic regression with Neural Network
이번에는 조금 다른 방법으로 TensorFlow를 사용하여 신경망을 이용한 로지스틱 회귀(Logistic regression)을 모델을 학습시켰습니다.
import tensorflow as tf
import tensorflow.keras.layers as layers
import tensorflow.keras.models as models
n_inputs = x_train.shape[1]
n_output = 2
model_nn = tf.keras.Sequential([
layers.Dense(64, input_shape=(n_inputs, ), activation='tanh'),
layers.Dense(32, activation='relu'),
layers.Dense(16, activation='relu'),
layers.Dense(n_output, activation='softmax'),
])
model_nn.compile(loss = 'sparse_categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
model_nn.summary()
# train
model_nn.fit(x_train, y_train, batch_size=100, epochs=10, validation_data=(x_test, y_test))
# predict
y_pred = model_nn.predict(x_test)
y_real = y_test
# Model: "sequential_1"
# _________________________________________________________________
# Layer (type) Output Shape Param #
# =================================================================
# dense_4 (Dense) (None, 64) 1856
# _________________________________________________________________
# dense_5 (Dense) (None, 32) 2080
# _________________________________________________________________
# dense_6 (Dense) (None, 16) 528
# _________________________________________________________________
# dense_7 (Dense) (None, 2) 34
# =================================================================
# Total params: 4,498
# Trainable params: 4,498
# Non-trainable params: 0
# _________________________________________________________________
# Epoch 1/10
# 1994/1994 [==============================] - 4s 2ms/step - loss: 0.0213 - accuracy: 0.9928 - val_loss: 0.0030 - val_accuracy: 0.9994
# Epoch 2/10
# 1994/1994 [==============================] - 4s 2ms/step - loss: 0.0031 - accuracy: 0.9994 - val_loss: 0.0029 - val_accuracy: 0.9993
# ...
# Epoch 10/10
# 1994/1994 [==============================] - 4s 2ms/step - loss: 0.0016 - accuracy: 0.9995 - val_loss: 0.0030 - val_accuracy: 0.9995
y_pred = y_pred.argmax(axis=1)
accuracy = round(sum(y_pred == y_real) / len(y_pred), 4)
print('Accuracy : ', accuracy)
print(classification_report(y_real, y_pred))
# Accuracy : 0.9995
# precision recall f1-score support
# 0 1.00 1.00 1.00 85303
# 1 0.93 0.74 0.83 140
# accuracy 1.00 85443
# macro avg 0.96 0.87 0.91 85443
# weighted avg 1.00 1.00 1.00 85443
RandomForest vs Logistic Regression
위에서 2가지 모델을 학습한 결과는 아래와 같습니다. 물론, 하이퍼 파라미터들을 어떻게 변경시키느냐에 따라 많이 바뀌겠지만 개념적으로 접근해보겠습니다.
| NO | Model | Precision | Recall | F1score | train-test rate |
|---|---|---|---|---|---|
| 1 | RandomForest | 0.93 | 0.77 | 0.84 | 7:3 |
| 2 | Logistic Regression | 0.93 | 0.74 | 0.83 | 7:3 |
두 모델 모두 F1-Score가 80% 이상으로 나름대로 좋은 성능을 보여줍니다. 하지만 우리가 실제로 사기 거래라는 것을 모른다면 어떻게 해야 할까요? 모든 거래를 판단할 수 없겠지만 극히 일부 데이터가 사기거래라고 알아냈다면 과연 학습이 될까요? 위와 완전히 동일한 모델로 train-test 비율은 1:9로 다시 학습해보면 아래와 같이 나타납니다.
| NO | Model | Precision | Recall | F1score | train-test rate |
|---|---|---|---|---|---|
| 1 | RandomForest | 0.80 | 0.63 | 0.71 | 1:9 |
| 2 | Logistic Regression | 0.28 | 0.78 | 0.41 | 1:9 |
RandomForest는 70%로 나름대로 유지했지만 두 모델 모두 성능이 안좋아집니다. 만약 사기 거래데이터가 더 적어지면 훨씬 급격하게 떨어집니다.
그래서 학습 데이터가 적은 경우에도 적용 가능한 모델을 찾고 싶어집니다.
Modeling 3 - Autoencoder
이번에는 신경망을 이용한 오토인코더(Autoencoder)로 학습을 시켜보고자 합니다.
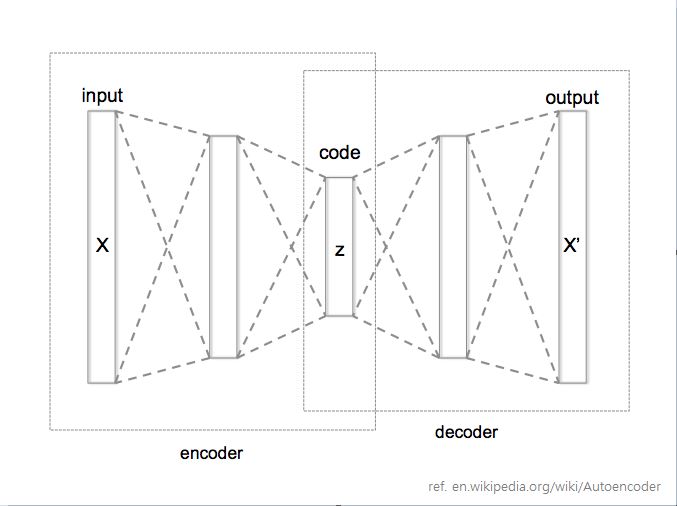
오토인코더를 간단하게 설명하면 기존 신경망 네트워크를 조금 특별한 구조로 구성하는 것인데요. 입력 데이터와 출력 데이터를 같게 하고 중간에 레이어 넣어 원복하게 만드는 구조입니다.
그림과 같이 인코더(encoder)와 디코더(decoder)를 통해 마치 압축했다가 압축해제하여 결과가 같도록 학습하는 것입니다. 즉 입력 데이터들에 대한 일종의 패턴을 찾아내는 것입니다. 중간에 있는 레이어를 보통 Latent vector 라고 표현합니다. 마치 입력데이터를 가지고 신경망에게 “알아서 vector로 표현해봐” 라고 하는 느낌입니다.
이 오토인코더에 정상 거래 데이터만을 학습시키면 정상 거래만 원복하는 패턴을 인지하는 모델을 생성하고 이 모델에 정상 거래를 넣으면 잘 원복할 것이고, 사기 거래는 잘 원복이 되지 않는 현상이 발생할 것입니다.
그 다음 Logistic Regression 모델을 이용하여 정상거래와 사기거래가 오토인코더에 넣었을 때 값을 기반으로 분류할 수 있도록 구성할 것입니다.
먼저 적은 양의 학습데이터만을 가지기 위해 train-test 비율을 1:9 로 생성합니다.
n_train = int(len(x_data) * 0.1)
x_train = x_data[:n_train]
y_train = y_data[:n_train]
x_test = x_data[n_train:]
y_test = y_data[n_train:]
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
# (28480, 28)
# (28480,)
# (256327, 28)
# (256327,)
오토인코더의 구조를 각 레이어(28 > 100 > 50 > 100 > 28)가 되도록 구성하였습니다. 그럼 28개의 Feature 정보가 레이어를 통해 다시 원복되는 패턴을 학습하게 됩니다.
여기서 정상 데이터만을 넣어 학습시키게 합니다.
import tensorflow as tf
import tensorflow.keras.layers as layers
import tensorflow.keras.models as models
n_inputs = x_train.shape[1]
n_outputs = 2
n_latent = 50
inputs = tf.keras.layers.Input(shape=(n_inputs, ))
x = tf.keras.layers.Dense(100, activation='tanh')(inputs)
latent = tf.keras.layers.Dense(n_latent, activation='tanh')(x)
# Encoder
encoder = tf.keras.models.Model(inputs, latent, name='encoder')
encoder.summary()
latent_inputs = tf.keras.layers.Input(shape=(n_latent, ))
x = tf.keras.layers.Dense(100, activation='tanh')(latent_inputs)
outputs = tf.keras.layers.Dense(n_inputs, activation='sigmoid')(x)
# Decoder
decoder = tf.keras.models.Model(latent_inputs, outputs, name='decoder')
decoder.summary()
# 정상 데이터 만을 학습
x_train_norm = x_train[y_train == 0]
autoencoder = tf.keras.models.Model(inputs, decoder(encoder(inputs)))
autoencoder.compile(optimizer='adam', loss='mse')
autoencoder.fit(x_train_norm, x_train_norm, epochs=15, batch_size = 100, validation_data=(x_test, x_test))
# Model: "encoder"
# _________________________________________________________________
# Layer (type) Output Shape Param #
# =================================================================
# input_19 (InputLayer) [(None, 28)] 0
# _________________________________________________________________
# dense_86 (Dense) (None, 100) 2900
# _________________________________________________________________
# dense_87 (Dense) (None, 50) 5050
# =================================================================
# Total params: 7,950
# Trainable params: 7,950
# Non-trainable params: 0
# _________________________________________________________________
# Model: "decoder"
# _________________________________________________________________
# Layer (type) Output Shape Param #
# =================================================================
# input_20 (InputLayer) [(None, 50)] 0
# _________________________________________________________________
# dense_88 (Dense) (None, 100) 5100
# _________________________________________________________________
# dense_89 (Dense) (None, 28) 2828
# =================================================================
# Total params: 7,928
# Trainable params: 7,928
# Non-trainable params: 0
# _________________________________________________________________
# Epoch 1/15
# 284/284 [==============================] - 3s 12ms/step - loss: 0.9139 - val_loss: 0.8323
# Epoch 2/15
# 284/284 [==============================] - 3s 11ms/step - loss: 0.7964 - val_loss: 0.7934
# Epoch 3/15
# 284/284 [==============================] - 3s 12ms/step - loss: 0.7796 - val_loss: 0.7795
# ...
# Epoch 14/15
# 284/284 [==============================] - 3s 11ms/step - loss: 0.7592 - val_loss: 0.7481
# Epoch 15/15
# 284/284 [==============================] - 3s 11ms/step - loss: 0.7589 - val_loss: 0.7478
오토인코더의 인코더에 train 데이터를 넣은 결과로 나온 Latent Vector로 정상 거래, 사기 거래 중 무엇인지 분류하도록 학습합니다.
encoded = encoder.predict(x_train)
classifier = tf.keras.Sequential([
layers.Dense(32, input_dim=n_latent, activation='tanh'),
layers.Dense(16, activation='relu'),
layers.Dense(n_outputs, activation ='softmax')
])
classifier.compile(loss='sparse_categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
classifier.summary()
classifier.fit(encoded, y_train, batch_size=100, epochs=10)
# Model: "sequential_15"
# _________________________________________________________________
# Layer (type) Output Shape Param #
# =================================================================
# dense_102 (Dense) (None, 32) 1632
# _________________________________________________________________
# dense_103 (Dense) (None, 16) 528
# _________________________________________________________________
# dense_104 (Dense) (None, 2) 34
# =================================================================
# Total params: 2,194
# Trainable params: 2,194
# Non-trainable params: 0
# _________________________________________________________________
# Epoch 1/10
# 285/285 [==============================] - 0s 1ms/step - loss: 0.0641 - accuracy: 0.9884
# Epoch 2/10
# 285/285 [==============================] - 0s 1ms/step - loss: 0.0068 - accuracy: 0.9980
# ...
# Epoch 9/10
# 285/285 [==============================] - 0s 1ms/step - loss: 0.0038 - accuracy: 0.9986
# Epoch 10/10
# 285/285 [==============================] - 0s 1ms/step - loss: 0.0036 - accuracy: 0.9988
# Predict !
pred_y = classifier.predict(encoder.predict(x_test)).argmax(axis=1)
y = y_test
print(classification_report(y, pred_y))
# precision recall f1-score support
# 0 1.00 1.00 1.00 255928
# 1 0.83 0.77 0.80 399
# accuracy 1.00 256327
# macro avg 0.91 0.89 0.90 256327
# weighted avg 1.00 1.00 1.00 256327
비교적 적은 학습데이터로도 f1-score가 80%에 달하는 좋은 모델을 만들었습니다.
최종 학습 결과
| NO | Model | Precision | Recall | F1score | train-test rate |
|---|---|---|---|---|---|
| 1-1 | RandomForest | 0.93 | 0.77 | 0.84 | 7:3 |
| 2-1 | Logistic Regression | 0.93 | 0.74 | 0.83 | 7:3 |
| 1-2 | RandomForest | 0.80 | 0.63 | 0.71 | 1:9 |
| 2-2 | Logistic Regression | 0.28 | 0.78 | 0.41 | 1:9 |
| 3 | Autoencoder + Logistic Regression | 0.83 | 0.77 | 0.80 | 1:9 |
Higly unbalanced한 데이터셋은 일반적으로 학습 데이터를 잘 수집할 수 있으면 나름대로 좋은 예측 모델을 만들어 낼 수 있습니다. 그런데 실제 현실은 레이블링이 되어 있는 데이터가 없는 경우가 많습니다. 이러한 경우 어떤 방식으로 접근을 해야될 지, 그리고 이렇게 만든 모델을 어떻게 평가할 수 있는지에 대해 정리해보았습니다.
.JPG)