[알고리즘 설계] 4. 탐욕법(Greedy)
in Problem Solving on Algorithm
탐욕법은 보통 최적해를 구하기 어려울 때 근사해를 찾는 방법입니다. 하지만 특정 조건에서는 탐욕법으로도 최적해를 구할 수 있는데 이런 경우 알고리즘 문제로 등장하기도 합니다. 탐욕법을 이해할 수 있도록 몇 가지 예제를 통해 설명하고 연습문제를 풀어보면서 직접 구현해보는 것이 목표입니다.
탐욕법 (Greedy)
탐욕법(Greedy)은 완전탐색과 동적계획법처럼 모든 경우를 탐색하여 계산한 결과를 바탕으로 구하는 것이 아니라 매순간 가장 좋은 선택(지역적인 최적해)만 하는 것을 말합니다.
최단경로를 찾는 문제를 예로 들면, 서울에서 부산까지 최단경로를 찾기위해 모든 경로를 탐색해보는 것이 아니라 서울에서 현재 갈 수 있는 지역 중 가장 가까운 도로만을 이용하면서 부산에 도달할 때까지 경로를 찾을 수 있습니다. 이렇게 탐색하면 당연히 훨씬 빠르게 계산할 수도 있고 최단경로에 꽤 가까운 답을 낼 수 있겠지만, 실제 최단경로는 아닐 가능성이 높습니다. 이처럼 대부분의 문제는 탐욕법으로는 최적해를 구할 수 없지만 근사해를 구해야할 경우 유용하게 사용될 수도 있습니다.
그런데 탐욕법도 어떤 조건 하에서는 최적해일 수 있습니다. 그래서 우리는 탐욕법이 최적해를 구할 수 있는 이 조건에 대해서 깊게 고민해볼 것입니다.
탐욕법에서 최적해를 구할 수 있으려면 2가지 조건이 성립해야 합니다.
탐욕법의 최적해 조건
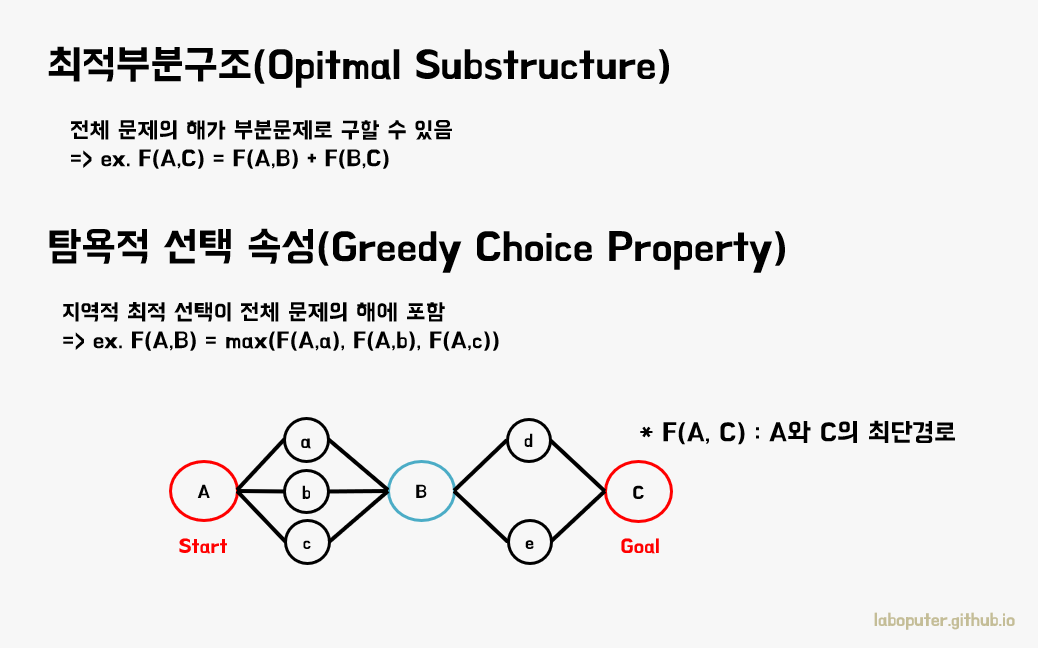
- 최적부분구조(Optimal Substructure)
- 전체문제의 해를 부분문제들의 해만으로도 구할 수 있게 분할가능한 구조
- 탐욕적 선택 속성(Greedy Choise Property)
- 지역적인 최적의 선택이 전체문제의 해에 반드시 포함됨
최적부분구조는 동적계획법에서 적용하기 위한 조건 중 하나와 같은 것입니다. 다시 설명하면 그림과 같은 그래프에서 F(A,C)를 구하기 위해 F(A,B) 와 F(B,C)의 합으로 구할 수 있습니다. 전체 부분문제들도 모두 위와 같이 부분문제의 합으로 구할 수 있습니다. 이런 경우를 최적부분구조가 성립한다고 표현합니다.
탐욕적 선택 속성은 그림처럼 F(A,B)를 구할 때 A의 입장에서 가장 가까운 길을 선택해도 F(a, B), F(b,B), F(c, B) 와 관계 없이 F(A,B)의 해에 포함되는 것을 말합니다. 이러한 속성이 모든 부분문제에 대해 적용되면 우리는 탐욕적 선택 속성이 성립한다고 말합니다.
이 두 가지 속성이 성립하면 당연히 탐욕법은 최적해를 구할 수 있게 됩니다. 왜냐하면 탐욕적 선택 속성에 의해 현재 상태에서 최적의 선택이 최종 선택의 해에 포함되며 최적부분구조에 의해 부분 문제의 해만으로 전체 문제의 최적해를 구할 수 있기 때문입니다.
탐욕법 사고연습
예제1. 동전 종류가 4가지(10원, 50원, 100원, 500원)이 있을 때, N 원을 가지기 위한 최소 동전의 개수는?
단, N은 1억 이하
완전탐색 접근:
4가지 동전을 한번씩 사용해보는 재귀를 이용해서 모든 경우를 탐색할 수 있습니다. 하지만 시간복잡도가 O(4^x) 로 지수승에 가깝습니다.
x 값은 구하기 쉽지 않지만 500원을 기준으로 해도 1억/500 = 20만으로 매우 큰 값입니다.
동적계획법 접근:
d[N] : N원을 표현하는 최소 동전 개수
이렇게 문제를 정의하면 관계식도 쉽게 찾을 수 있습니다. 하지만 N의 값이 아주 크기 때문에 메모리로 표현하기 어렵고, N의 값이 크다는 것은 구해야 하는 부분문제도 종류가 많다는 것을 의미합니다. 이 방법도 좋은 방법은 아닌 것 같습니다.
탐욕법 접근:
먼저 탐욕법으로 해결 가능한지 확인하기 위해 2가지 속성이 성립하는지 확인해야 합니다.
F(n) = 1 + min(F(n-10), F(n-50), F(n-100), F(n-500))
최적부분구조는 위와 관계식으로 쉽게 증명됩니다.
N보다 작은 가장 큰 동전을 사용한 최적해가 반드시 존재한다.
위의 의미를 좀 더 풀어서 설명하면 N 이 500 보다 크면 반드시 500원 짜리 동전을 사용하는 것이 좋습니다. 왜냐하면 500원을 표현할 때 다른 동전으로는 절대로 적은 개수로 표현할 수 없기 때문입니다. 즉 탐욕적 선택 속성이 성립합니다.
그렇기 때문에 이 문제는 4가지 동전을 하나씩 사용하면서 탐색해볼 것이 아니라 가장 큰 동전만을 계속 선택해도 최적해를 구할 수 있습니다.
그러면 시간복잡도는 O(1) 입니다.
int coins[4] = {500, 100, 50, 10};
int count = 0;
for(int i=0; i<4; i++)
{
if (N / coins[i])
{
count += N / coins[i];
N %= coins[i];
}
}
// Result
printf("%d\n", count);
위와 같은 예제가 조건이 살짝 바뀌어 동전의 종류가 400원 짜리가 하나 추가되면 어떻게 될까요?
예제 1-2: 동전 종류가 5가지 (10원, 50원, 100원, 400원, 500원) 이라면?
이 문제는 최적부분구조가 성립하지만, 탐욕적 선택 속성이 성립하지 않기 때문에 탐욕법으로 풀 수 없습니다.
N = 800 인 경우, 위의 탐욕법으로 계산하면 4 (500원1, 100원3) 이지만 최적해는 2 (400원*2) 입니다. 탐욕적 선택 속성이 성립하지 않기 때문에 지역적 최적의 선택이 최적해를 포함하지 않습니다.
이 문제에서 탐욕적 선택 속성이 성립하려면 모든 동전의 종류가 각 동전의 배수여야 합니다. 그래야만 작은 동전을 X개 사용했을 때 더 큰 동전으로 대체할 수 있기 때문입니다.
이렇게 탐욕법은 2가지 속성만 확인되면 아주 빠른 속도로 해를 구할 수 있습니다.
연습문제
문제 링크:: ATM (https://www.acmicpc.net/problem/11399)
자세한 문제 설명은 위 링크로 들어가셔서 확인하시고 직접 풀어보세요!
이 문제는 모든 사람이 줄 서는 순서에 따라 대기시간이 달라지는데 이 대기시간을 최소화하는 문제입니다.
풀이
이 문제는 좋은 아이디어 하나만 캐치하면 쉽게 푸실 수 있습니다.
인출시간이 가장 짧은 사람이 제일 먼저 인출하게 하면 됩니다. 왜냐하면 앞에서 인출한 사람의 시간이 뒷사람에 모두 누적되니까요.
수식으로 표현하면 총 대기시간은 아래와 같습니다.
# a[n]: n번째 사람이 인출한 시간이라고 할때,
answer : a[0] * n + a[1] * (n-1) + ... + a[n-1]*1
가장 인출시간이 짧은 사람부터 인출하면 그 선택이 최적해에 반드시 포함되기 때문에 탐욕적 선택 속성을 만족합니다. 그리고 최적부분구조는 직관적으로도 쉽게 성립함을 알 수 있습니다.
즉 이 문제는 탐욕법으로 가장 짧은 인출시간을 가진 사람부터 인출하기 위해, 오름차순으로 정리한다음 전체시간만 구하면 됩니다.
시간복잡도는 정렬하는 것에 지배적이기 때문에 O(NlogN) 입니다.
전체 코드:
#include <stdio.h>
#include <algorithm>
using namespace std;
#define MAXN 1005
int a[MAXN];
int N;
int main(void)
{
scanf("%d", &N);
for (int i = 0; i < N; i++) scanf("%d", &a[i]);
sort(a, a + N);
int sum = 0;
int ans = 0;
for (int i = 0; i < N; i++)
{
sum += a[i];
ans += sum;
}
printf("%d\n", ans);
return 0;
}
다른 연습문제 추천
- 행렬: (https://www.acmicpc.net/problem/1080)
- 회의실 배정: (https://www.acmicpc.net/problem/1931)
그리디 문제는 알고리즘을 전혀 몰라도 쉽게 접근가능하긴 하지만 어려운 문제에 속하는 것들은 탐욕적 선택 속성을 만족하는 아이디어를 찾는 것이 결코 쉽지는 않습니다. 그저 많이 풀어보는게 답인듯 합니다.